Pokušaji da se dođe do odgovora na navedeno pitanje pokazuju se, bar u početku, kao prilično mukotrpni, ako ne i iluzorni.Ceo svet (bar onako kako se nama predstavlja taj „ceo svet”) koristi arapske, a sami Arapi koriste neke druge cifre? I kako je do toga došlo? Iako će se teško ikada doći do odgovora na ovo pitanje, ali i na slična pitanja, ono je korisno jer otvara vidike. Pokazuje se da ni s ciframa (brojevima), iako su one „univerzalne”, nije sve tako jednostavno.

Prof. dr Rajko M. Bukvić
Za obeležavanje brojeva (i sve operacije s njima) u savremenim brojčanim sistemima koriste se cifre. Iako se u svakodnevnom životu neretko upotrebljavaju kao sinonimi, cifra i broj nisu identični, oni se razlikuju i po značenju i po poreklu.[1] Kao cifre, dakle znaci kojima se obeležavaju brojevi, u najvećem delu sveta, koriste se danas tzv. arapske cifre. Na njih smo svi mi do te mere navikli da najčešće i ne pomišljamo da mogu postojati (i da su nekada postojale i da i danas postoje) i nekakve druge cifre.
Evropljane je s tim
ciframa upoznao rimski
papa Silvester II.
Za razliku od slova i slovnih sistema, koji se uzgred razlikuju od jednog do drugog jezika, i to ne samo po vrsti pisma već i po broju znakova koji se u tim sistemima koriste, postojanje arapskih cifara predstavlja nam se kao univerzalno, nešto što čini opšte dobro i dostignuće cele ljudske civilizacije.
Mali izuzetak su rimske cifre (i rimski brojevi), s kojima se većina nas upoznala u školi, i koje još uvek možemo videti na nekim starijim zdanjima (vid. sl. 1, koja pokazuje godinu izgradnje Beogradske železničke stanice), ili i u savremenim knjigama i drugim tekstovima, na primer u ispisivanju rednih brojeva meseci ili vekova. Međutim, oni se ipak tretiraju kao nekakav relikt, koji ne dovodi u pitanje prethodno istaknuto. A upravo zbog toga i ne zamišljamo se nad eventualnim pitanjima da li je to baš tako, a i kad bi bilo tako – ko je i šta je doprinelo da te cifre postanu takve, univerzalne.
Zbrka na internetu
Sve je to ukupno uzev dosta čudno, posebno u našoj eri kompjutera i interneta. Dovoljno je, naime, samo malo zaći van uobičajenih („zapadnih”, odnosno uglavnom evropskih) sajtova, ili uzeti u ruke neke druge novine ili knjige, pa se naći u nedoumici. Na primer, poseta nekog arapskog ili indijskog sajta mnoge od nas će iznenaditi činjenicom da se tamo ne mogu naći „arapske” cifre i brojevi. (Vidi sl. 2 na kojoj možemo u drugom redu prepoznati brojeve koji se razlikuju od slova time što ne „vise” na horizontalnoj liniji. Umesto njih, nama poznatih – „arapskih”, pojavljuju se neke druge cifre (najčešće one prikazane na sl. 3, druga i treća kolona; komentar u kasnijem tekstu). Otkud sad to, pitanje se samo nameće – ceo svet (bar onako kako se nama predstavlja taj „ceo svet”) koristi arapske, a sami Arapi koriste neke druge cifre? I kako je do toga došlo? Iako će se teško ikada doći do odgovora na ovo pitanje, ali i na slična pitanja, ono je korisno jer otvara vidike. Pokazuje se da ni s ciframa (brojevima), iako su one „univerzalne”, nije sve tako jednostavno.
Danas se smatra da je
arapski svet s indijski
ciframa upoznao čuveni
matematičar Al Horezmi,
čije se jedno delo naziva
„Knjiga o indijskom računu”.
Pokušaji da se dođe do odgovora na navedeno pitanje pokazuju se, bar u početku, kao prilično mukotrpni, ako ne i iluzorni. Autoritetna sovjetska Matematička enciklopedija[2] navodi pod odrednicom „Arapske cifre” da je to tradicionalan naziv za skup od deset matematičkih znakova (0, 1, … 9), pomoću kojih se u desetnom brojčanom sistemu zapisuju brojevi, i da su te cifre nastale u Indiji (ne posle 5. veka), a da su u Evropi postale poznate u periodu 10-13 v. na osnovu (prevedenih) arapskih dela.[3] Danas se smatra da je arapski svet s indijskim ciframa upoznao čuveni matematičar i naučnik Al Horezmi (783-850), čije se jedno delo upravo tako i naziva: „Knjiga o indijskom računu”[4]. A Evropljane je s tim ciframa upoznao rimski papa Silvester II (Herbert Avrilački ili Orilački, Herbert Rejmski, ok. 946-1003, papa od 999), zahvaljujući vezama koje su tada postojale s arapskim halifatom u Kordovi, na teritoriji današnje Španije.
Dakle, po toj, možemo reći – opšteprihvaćenoj, slici (verziji) arapske cifre su nastale u Indiji i u Evropu su ih preneli arapski autori (matematičari), s čijim su se delima upozna(va)li tadašnji Evropljani. Ipak, treba naglasiti da je i pored toga konstantno, još od srednjeg veka, trajao spor o indijskom poreklu arapskih cifara, i već tada nije postojalo čvrsto uverenje u ovu teoriju, a sporovi su bivali pojačavani činjenicom da je već krajem 11. veka počelo falsifikovanje „drevnih indijskih” cifarskih zapisa[5]. Usled toga, u 13. veku na zapadu Evrope prestali su da smatraju Indiju kolevkom ovih cifara, a zaslugu njihovog stvaranja preneli su na Arape (verovatno, otuda i potiče naziv „arapske cifre”), koji, međutim, na to nikada nisu pretendovali! Veliki broj lažnih (falsifikovanih) natpisa još i danas otežava istraživanja porekla „arapskih” cifara.[6] Ipak, ostaje ovde istaknuto pitanje – zašto se naše uobičajene, dakle arapske cifre ne koriste ni u arapskim zemljama ni u Indiji, već se u njima koriste drugačije cifre (sl. 3)?
Zapravo, samo malo „šetnje” po internetu dovešće nas do (malo) veće zbrke – pokazuje se da se danas koristi, odnosno da se tokom istorije koristio veći broj različitih vrsta cifara, odnosno brojeva i brojčanih sistema (vid. sl. 4). Pri tome, u ovoj tabeli Inženjerskog priručnika DPVA navedeni su i pozicioni i nepozicioni sistemi, pri čemu svi pozicioni sistemi kao osnovu imaju broj deset (10). Problem osnove brojčanih sistema u ovom tekstu nećemo razmatrati. Podvući ćemo samo da je očigledno da je nastanak pozicionih brojčanih sistema i savremenih („arapskih”) cifara očigledno međusobno uslovljen.
১১ অগ্রহায়ণ ১৪২৩ রবিবার ২৭ নভেম্বর ২০১৬
![]()
Slika 2. Zaglavlje novina na bengalskom
Izvor: http://www.anandabazar.com
Iz nekog razloga, međutim, u ovoj tabeli (sl. 4) ne nalazi se i slovenski brojčani sistem (sl. 5), koji se u dobrom delu „preklapa” s grčkim (jonskim) sistemom. Praktično, jedina razlika je, kako se vidi, što grčki sistem koristi velika, a slovenski mala slova. Pored toga, razliku čini slovo C, koje je zamenilo grčko slovo sampi Ϡ (Ϡ) — tog kako kažu strašnog, još do Arhimeda izumrlog krѧkozяbra (krakozjabra, ili krjakozjabra)[7]. Usled toga, s pravom se kaže da je slovenski sistem prekopiran s grčkog, što se vidi i po tome što negrčkim slovima iz slovenske azbuke (B, Ž, Š, Щ, Ъ, Ы, Ь, Ю, Я, Ѣ, Ѫ, Ѧ) nisu bile dodeljene brojne vrednosti, isključujući početni pokušaj da se slovu ens Ѧ (mali jus) dodeli vrednost 900. Pored toga, vremenom je došlo do nekih manjih promena (ižica Ѵ, iz koje je nastalo slovo U, vremenom joj je ustupila vrednost 400, koju je sama dobila od ipsilona Υ; slovo Č, s vrednošću 90 nastalo je iz doistorijske kope Ҁ, preko slova zi Ϟ; stigma se promenila u zagogulinu Ϛ, davši na kraju zelo Ѕ s istom vrednošću 6).[8]

Slika 3. Savremeni cifarski brojčani sistemi
U konačnom vidu slovenski brojni sistem ustalio se prema prikazu na slici 4. Njegove osnovne karakteristike su: dvadeset sedam slova s brojnim vrednostima (po devet u svakom razredu – jedinice, desetica i stotine), i odsustvo nule. Uz pomoć ovih slova mogao se zapisati svaki broj od 1 do 999, a da bi se brojevi razlikovali od običnog teksta, korišćen je posebni znak ~ (titla, odnosno preciznije rečeno cifarska titla, pošto je titla korišćena i za neke druge potrebe, na primer za skraćivanje reči). Titla se po nekim tumačenjima pisala iznad pretposlednjeg slova (posmatrano sleva na desno), a po drugim iznad celog brojnog zapisa, ili pak iznad svake od „cifara” (slova). Svakoj našoj cifri (izuzimajući nulu, dakle – 1, 2, 3 …) odgovarala su po tri slova, zavisno od razreda u kome se ta „cifra” nalazi (sl. 5).
Treba obratiti pažnju da su razredi (tj. slova koja njima pripadaju) pisani po ustaljenom redosledu: stotine, desetice, jedinice (sleva na desno), dakle onako kako se pišu u savremenom pozicionom sistemu. Izuzetak su brojevi u prvoj desetici (11-19), gde se prvo upisuju slova iz prvog, a zatim iz drugog razreda, dakle onako kako je pokazano na slici 7. Nama to danas može izgledati čudno, ali samo ako ne obratimo pažnju na nazive odgovarajućih brojeva (jedanaest, dvanaest itd., odnosno jedan na deset, dva na deset itd.). Za brojeve preko 999 korišćena su ista slova, ali u kombinaciji s posebnim znacima. Tako je hiljada obeležavana znakom ҂ koji je pisan ispred prve cifre (slova) s leve strane, i niže od nje (poput indeksa, ili subskripta). Znak se odnosio samo na prvo slovo koje mu sledi, tako da se zapis brojeva u kojima se nalazi više od devet hiljada odlikovao višestrukom upotrebom ovog znaka (vid. sl. 5). I za veće brojeve, koji su imali naročite nazive – tma, legeon (ili nesved), leodr, voron, koloda, zakolodje – korišćena su ista slova, ali obeležena posebnim znacima (sl. 6).[9] Naravno, postojalo je i ono što se danas popularno zove „dubleti”, pa se tako veliki brojevi mogu pisati na dva (nekad i tri) načina.[10]

Slika 4. Razni nepozicioni i pozicioni numerički sistemi
Izvor: http://www.dpva.ru/Guide/GuideMathematics/GuideMathematicsNumericalSystems/DecimalNumeralsVarious/
Slovenski alfavitni sistem održao se u Rusiji do 17. veka, da bi početkom i tokom 18. veka, posle reformi Petra Velikog, preovladao sistem arapskih cifara. Što se nas tiče, prema Srpskoj enciklopediji[11] „od zvaničnog početka srpske pismenosti u IX veku b[rojevi] su se zapisivali slovnom numeracijom po ugledu na vizantijski sistem i staroslovensku numeraciju”. Onoga ko pomisli da je reč o sistemu prikazanom na sl. 5 sledeća konstatacija će zbuniti: „U Bukvaru Inoka Save iz 1597. taj zapis je prilagođen ćiriličnim slovima.”(!) Šta sad to znači, kakav je do tada bio zapis? Možda autor odrednice misli na slova glagoljice? Ali, čemu onda tu pominjanje vizantijskog sistema? I ako se na to misli, zašto se to ne kaže?
Dalje, u tekstu piše: „Potpuni sistem arapskih cifara i osnovnih operacija s b[rojevima] zapisanim tim ciframa dat je u prvoj srpskoj aritmetici V. Damjanovića iz 1767. U Vukovom bukvaru iz 1827. uporedo su dati tzv. znaci b[rojeva]: „crkveni” b[rojevi] (nepoziciona slovna numeracija), arapski („obični”) b[rojevi] (poziciona dekadna numeracija) i rimski („latinski”) b[rojevi]”. Iako nije tako eksplicitno rečeno, treba pretpostaviti da je reč o prvom (potpunom) pojavljivanju arapskih cifara (kod Damjanovića), dok smisao pominjanja Vukovog rečnika ovde nije jasan. Sve u svemu, iz ovog izvora, koji bi po definiciji trebalo da bude autoritetan, ne može se takoreći ništa saznati.

Slika 5. Staroslovenske cifre i brojevi
Da bismo mogli (ili bar pokušali) da odgovorimo na početno pitanje o nastanku arapskih cifara, potrebna su očigledno još neka objašnjenja. Pre svega, šta je broj(ča)ni sistem, ili sistem numeracije, odnosno pod kakvim se sve terminima ovaj pojam može pronaći u literaturi. Citirana sovjetska Matematička enciklopedija[12], u odrednici Sčislenie (brojanje, računanje), definiše brojanje (numeraciju) kao ukupnost načina predstavljanja prirodnih brojeva. Pri tome, u svakom sistemu numeracije neki su simboli (reči ili znaci) čvorni, dok se ostali (algoritamski) dobijaju iz njih kao rezultat nekakvih operacija. Brojčani sistemi se razlikuju po izboru čvornih brojeva i po načinu obrazovanja algoritamskih. S pojavom pisanih znakova brojčanih simbola brojčani sistemi su se počeli razlikovati po karakteru brojčanih znakova i po principima njihovih zapisa.
Od svih karakteristika i podela brojčanih sistema nas će u daljem interesovati alfavitni sistemi (grčko-slovenski) i pozicioni sistemi. Grčko-slovenski brojčani sistem se često označava kao polupozicioni, ali (ne)opravdanost takve karakteristike nije od daljeg našeg interesa. Savremeni brojčani sistemi (sa 10 uobičajenih, ili arapskih, ili indijskih cifara) spadaju u pozicione sisteme. Naravno, pozicioni brojčani sistemi mogu imati (i u praksi se to neretko dešavalo i dešava) i manje ili više cifara od deset.[13] Štaviše, moglo bi se reći da su drugi sistemi preovlađivali (na primer, podela dana na 24 časa, podela godine na 12 meseci, podela minuta na 60 sekundi itd.) Osnovna karakteristika pozicionih brojčanih sistema, bez obzira na osnovu) jeste postojanje i korišćenje nule (simbol 0 u savremenoj notaciji, ili neki drugi odgovarajući, sl. 3). Očigledno, pozicioni brojčani sistemi i otkriće pojma nula nerazdvojno su povezani.
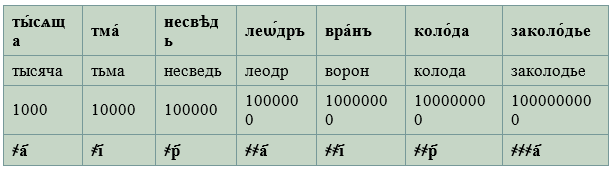

Slika 6. Veliki brojevi u slovenskom alfavitnom sistemu
Izvor: : Slavяnskie cifrы, http://www.konorama.ru/servisy/slacy/
Naše početno pitanje preraslo je, dakle, u pitanje: gde je i kada pronađen pozicioni brojčani sistem, odnosno gde je i kada otkrivena nula? U odgovoru na ovo pitanje istoričari (matematike) su saglasni[14]: pozicioni desetni sistem nastao je u Indiji, to je „najpoznatije dostignuće indijske matematike”, a desetni brojčani sistem ima „vrlo davno poreklo”, njegova „prva nama poznata primena (…) odnosi se na 595. godinu”, ali su „još mnogo pre toga Indijci posedovali sistem za usmeno izražavanje velikih brojeva, pri čemu se koristio princip pozicionosti”. Postoje, naime, i stariji tekstovi „u kojima se potpuno određeno koristi reč ‚sunja’, koja označava nulu”, a „najstariji pisani dokument sa znakom za nulu odnosi se na deveti vek”. Ali, ni to nije sve: „Sve to je znatno kasnijeg porekla od znaka nule u vavilonskim tekstovima.”

Slika 7. Staroslovenski brojevi prve desetice
Prema istom izvoru, desetni pozicioni sistem prodro je zatim karavanskim putevima u mnoge oblasti Bliskog istoka i počeo da se koristi uporedo s drugim sistemima. Postepeno, njega su počeli sve šire da koriste u arapskom svetu, pri čemu su se za zapis cifara koristili vrlo raznovrsni znakovi. Među njima se izdvajaju dva tipa: indijski znakovi, koji su primenjivani među istočnim Arapima i tzv. cifre gobar (ili gubar) koje su primenjivali zapadni Arapi u Španiji. Pri tome, „znakovi prvog tipa još i danas se primenjuju u arapskom svetu”, dok je „naš savremeni sistem, očevidno, proistekao iz sistema ‚gobar’”. O tome kako su cifre „gobar” prodrle u Španiju postoji nekoliko teorija, od kojih je najpoznatija Vepkeova, prema kojoj su one primenjivane u Španiji kada su tamo prodrli Arapi, ali su ih znatno ranije (oko 450. godine) neopitagorejci iz Aleksandrije preneli na Zapad.
Od drugih teorija (ili hipoteza) veliku popularnost je stekla hipoteza da (arapske) cifre tačno predstavljaju (pokazuju) broj uglova u njihovoj grafičkoj prezentaciji. Iako je kod nekih cifara doista tako, lako se vidi da se kod drugih taj efekt postiže vrlo teško, pri tome uz pomoć nekakvih dodatnih linija na osnovnu formu cifre (cifra 9, na primer, ili i 7, kako je pokazano u jednoj od varijanata u kojima se predstavlja ova „teorija”, slika 8). Naravno, ova hipoteza je nenaučna ne samo iz tog razloga, već pre svega zato što pretpostavlja kao tvorca „arapskih” cifara (u njihovom savremenom obliku) nekakvog apstraktnog mislioca koji rešava metafizičke zadatke. Pa ipak, na popularnim sajtovima na internetu se i danas može često sresti upravo ovakvo objašnjenje vezano za nastanak ovih cifara.

Slika 8. Nenaučna teorija o arapskim ciframa i broju uglova u njima
Kao kuriozitet može se navesti da se problemom porekla „arapskih” cifara bavio i veliki pisac Aleksandar Sergejevič Puškin. U njegovim rukopisima pronađena su razmatranja po kojima su cifre proizašle iz kvadrata, uz pomoć stranica i dijagonala kvadrata (vid. sl. 8). Puškinova hipoteza[15] danas se, takođe, često može sresti u raznim manje ili više popularnim tekstovima, a jedan od njih poslužio je kao izvor za sliku 9. Neistoričnost i previsok nivo apstrakcije može dozvoliti da se ni ova hipoteza, ipak, ne razmatra u našem tekstu. Umesto toga, pažnju može da privuče jedno drugo Puškinovo delo, njegova nedovršena Istorija sela Gorjuhina iz 1830[16]. Autor tog dela (Belkin, zapravo sam Puškin) pita se tu da li mu je potrebno, da bi se bavio istorijom, da uroni u letopise i da dopire do skrivenog smisla starog jezika kada nije bio u stanju da nauči slovenske cifre (str. 122).
Poznati sovjetski istoričar matematike Ivan Jakovljevič Depman, kome se inače u zaslugu ističe ideja da nisu sve „arapske” cifre nastale istovremeno, prihvatio je ovu Puškinovu sentencu kao dokaz da je nepoznavanje slovenske numeracije svojstveno ne samo ljudima našeg vremena[17]. Kao i celo delo, i ova Puškinova napomena vrlo je zagonetna – da li je on zaista imao u vidu sebe (tj. Belkina)? I da li je, i kako je moguće, nezavisno od prethodnog pitanja, da je u to vreme (1830) slovenska numeracija bila zaboravljena? Utoliko pre što je ona u Rusiji korišćena do 18. veka, ali i kasnije, doduše kasnije samo u crkvenim knjigama.[18] Istorija sela Gorjuhina može se pokazati kao izuzetno značajna upravo u ovom domenu, na primer ako se prihvati Strahovljeva hipoteza[19], prema kojoj je to, zapravo, najistaknutija Puškinova parodija, u kojoj je lažni Karamzinov ton u potpunosti razobličen.

Slika 9. Hipoteza A. S. Puškina o nastanku arapskih cifara
Izvor: S. Kapitonov, Arabskie čisla i A. S. Puškin, 2016.
Za nas je, međutim, važan poseban aspekt ove priče. Videli smo, naime, da je već pre dvestotinak godina aktuelno bilo zaboravljanje slovenske numeracije, bez obzira da li Puškinove reči tumačimo kao realnost (dakle, reč upućenu samom sebi) ili kao parodiju. Danas to svakako mora utoliko pre biti slučaj, ako ni zbog čega drugog, onda zato što se kod nas već decenijama (u našim školama, za razliku od škola u Kraljevini Jugoslaviji), staroslovenski jezik ne izučava. Između ostalog, zato se i dešava da se znak ҂ proglasi ne znakom za hiljadu, što je predstavljao (bio) u celom svetu koji je koristio staroslovensku numeraciju, već simbolom vremena kojeg je u srpske knjige prvi uneo Sveti Sava 6707. (1199. godine tzv. Hristove ere)[20]. Odnosno, simbolom kojim se označavaju godine, kako to sledi iz cele knjige, uključujući naslovnu stranu (na kojoj stoji: „Po srpskom kalendaru ҂ 7519. godina”), da bi najzad usledio i tekst sa sledećim nazivom: „Srećna Nova ҂ 7519. godina”! Šta, dakle, označava taj simbol? Apstraktni pojam vremena, ili je to znak za godinu tu i tu (tj. nešto konkretno)? I čemu, i u jednom i u drugom slučaju potreba da se pored tog simbola piše i reč „godina”?[21]

Slika 10. Rukopis Svetog Save iz Studeničkog tipika
Izvor: M. T. Stevančević, Heliocentrična meteorologija kao put za uspostavljanje Srpskog kalendara, str. 220.
Prošlost prekrivena vekovima i „ukrašena” mnogobrojnim falsifikatima još ni danas nije omogućila unošenje koliko-toliko izvesnosti u rešavanje pitanja nastanka „arapskih” cifara. Stvoren je veći broj hipoteza i teorija. Neke od njih izvodile su poreklo tih cifara 1) iz brzo i skladno napisanog odgovarajućeg broja štapića; 2) iz kruga s dvama perpendikularnim dijametrima; 3) iz kvadrata s diagonalama; 4) iz početnih slova odgovarajućih naziva brojeva u sanskritu; 5) iz latinskih stenografskih znakova, koje je pronašao ili usavršio Tiron, Ciceronov oslobođenik; 6) iz kineskih brojčanih hijeroglifa; 7) iz znakova pitagorejske simbolike; 8) iz slova alfavita: a) egipatskog hijeroglifskog, b) induskog, v) grčkog, g) persijskog, d) bakgrijskog.[22] Bilo je, naravno, i neistorijskih i nenaučnih hipoteza. Ali, kao konačan „rezultat” svih tih pokušaja ostaje činjenica da ne postoje hipoteze koje bi mogle da se smatraju konzistentnim i koje su, bar do sada, makar i minimalno izdržale probu vremena.
U okviru tog ne malog broja hipoteza i pretpostavki bilo je, kako je naglašeno, i pokušaja da se poreklo naših cifara dovede u vezu s različitim vrstama slova, koja se koriste, ili su se koristila u raznim jezicima i u raznim epohama. A u okviru toga i da se to poreklo objasni polazeći od slova grčkog alfabeta. Međutim, kako ističe Prohorov[23], pošto se polazilo od oblika slova redom (alfa, beta, gama itd.), ispostavljalo se da više ili manje sličnosti imaju samo sedmica (sa zetom), osmica (s etom) i devetka (s tetom). To je, naravno, bilo nedovoljno i hipoteza je napuštena. Sam Prohorov izneo je u tom tekstu istu hipotezu, ali ju je zasnovao na malo drugačijim pretpostavkama, ističući da je uvođenje nule u brojčani sistem moralo da izazove određena pomeranja u redosledu slova koja su postojala u tom brojčanom sistemu. Konkretno, postavio se problem – da li nulu za broj deset pripisati alfi-jedinici ili joti-desetki? Po autoru hipoteze logičnija je druga varijanta, i na taj način došlo je, po ovoj pretpostavci, do toga da jota preuzme mesto cifre 1.
Ako se to doista desilo, tada se pojavio „višak” znakova: za devet cifara postoji deset znakova (cifara). Jedan je morao da ispadne iz sistema, i izbor je pao na stigmu, kojom su Grci označavali cifru 6. Ona je već odavno služila samo kao ligatura, u alfabetu nije postojala. Stigma je, dakle, ispala iz sistema, a prvih pet slova-cifara (alfa, beta, gama, delta, epsilon) pomereni su za jedno mesto (preuzeli su „vrednosti” za jedan više). Tek sada, smatra Prohorov, moguće je upoređivati slova s ciframa (vid. sl. 11). Svoju hipotezu autor potkrepljuje i dodatnim argumentima, na osnovu paleografskih razmatranja, ali uz prethodnu, važnu napomenu – nas ne treba da interesuje uncijalni oblik grčkih slova (koji je dao formu savremenim velikim slovima). Iz čisto stilističkih svojstava (pravolinearnost, geometrijska pravilnost, svako slovo se upisuje u kvadrat) taj oblik nisu mogli da prihvate Arapi, oni su prihvatili pisana, kurzivna slova. To je poslovno pismo, uobičajeno za papirus i u vreme koje nas interesuje ono se rasprostranjuje i na pergament.

Slika 11. Hipoteza Prohorova
Izvor: G. M. Prohorov, Eщё odno mnenie o proishoždenii «arabskih» cifr, Trudы Otdela drevnerusskoй literaturы, 1969, Tom XXIV.
Hipoteza Prohorova je, naravno, interesantna, i svakako zaslužuje pažnju. Koju, po svoj prilici, nije dobila. Ali, nezavisno od toga, potrebno je naglasiti da napuštanje velikih slova zapravo pretpostavlja prelazak na slovenski brojčani sistem (vid. sl. 5). Njega, za razliku od grčkog, upravo karakteriše korišćenje malih slova. A i ona, normalno, imaju i kurzivnu formu. Ako učinimo takav korak, onda se približavamo hipotezi Nove hronologije, po kojoj su „arapske” cifre upravo i nastale od slova iz slovenskog alfavitnog brojčanog sistema. Proces pretvaranja slova u cifre, po hipotezi Nove hronologije, prikazan je na slici 12. Kao što se vidi na slici, a što Nosovski i Fomenko posebno podvlače[24], za stvaranje „arapskih” cifara korišćen je slovensko-grčki polupozicioni sistem numeracije, pri tome u mnogim slučajevima ruske skoropisne (brzopisane, tj. prosto pisane) forme ćiriličkih slova 16. veka. Na slici je to posebno istaknuto.

Slika 12. Poreklo arapskih cifara iz slovensko-grčkih slova-cifara posle otkrića nule
Izvor: G. V. Nosovskiй i A. T. Fomenko, Novaя hronologiя Rusi. Tom 2, Moskva, 2004, str. 229.
U ovoj hipotezi nekoliko momenata zaslužuje osobit osvrt. Najpre, to je cifra 2. Za nju nije korišćeno drugo slovo grčkog brojčanog sistema (beta, tj. vita), već B (buki), drugo slovo staroslovenske azbuke. Ovo je ključni moment cele hipoteze, pošto po Novoj hronologiji upravo to i predstavlja dokaz da nije korišćena grčka, već slovenska azbuka, tj. faktički slovenski alfavitni sistem. Kako je ilustrovano na sl. 12, u nekim slučajevima cifre su dobijene kao odrazi u ogledalu odgovarajućih slova (2 i 6), a u jednom – obrtom za 90⁰ (cifra 8).
Najzad, ostaje da se kaže nekoliko reči o ciframa 3 i 7, odnosno 5 i 6. Kao što je pokazano na slici 12, ove cifre su, u odgovarajućim parovima, zamenile mesta, tj. promenile svoje „brojčane” vrednosti. Zaista, za cifru 3 nema nikakve potrebe dokazivati da toliko liči na naše slovo Z, da se praktično i ne razlikuju. A Z (zeta) – to je slovo koje označava sedmicu u prvom razredu grčko-slovenskog alfavitnog sistema. Tu nema (ili ne bi trebalo da bude) nikakve dileme. S druge strane, sedmica je, po ovoj hipotezi, nastala od slovenskog T (skoropisna forma), koja je označavala trojku u trećem razredu. Sudeći po slici, i ovo je sasvim logično i razumljivo. Jedino u svem ovom razmatranju ostaje pitanje, kako je i zašto došlo do navedene promene. I u ovom, i u drugom istaknutom paru. U navedenom tekstu Nove hronologije[25], odgovor na to pitanje nije dat, konstatuje se samo da su tim ciframa iz nekog razloga zamenjena mesta. Slično je i s drugim parom, s ciframa 5 i 6. Uzeta su slova ε (epsilon) i ζ (zelo), koja su u alfavitnom sistemu imala „vrednosti” 5 i 6 (oba u prvom razredu), pri tome njihova skoropisna forma. Na kraju, kao i u prethodnom slučaju, došlo je iz nekih razloga do zamene mesta ovih dveju novostvorenih cifara.

Slika 13. Albreht Direr, Melanholija, gravira, 1514.
Izvor: www.yandex.ru/images›albrecht dürer melancholie
U oba slučajeva u kojima se konstatuje i ilustruje zamena mesta novostvorenim ciframa može se, i potrebno je, naravno, postaviti pitanje: koliko su i da li su te teze opravdane i dokazane? Čudinov u citiranom tekstu vrlo detaljno razmatra celu hipotezu Nove hronologije, između ostalog i to pitanje zamene mesta cifara. On, međutim, uz početnu ocenu da cela hipoteza ima pravo na postojanje, konstatuje da pretpostavka o zameni mesta navedenih dvaju parova cifara „nije dovršena”, ona „visi u vazduhu”.

Slika 14. Fragment Melanholije, magični kvadrat
Ipak, potrebno je naglasiti, pre svega, i to ne kao odgovor V. A. Čudinovu, da odsustvo dokaza ne zahteva nužno odbacivanje hipoteze, i da bi u tom smislu bilo nužno pronaći dokaze za njeno odbacivanje. A s druge strane, hipoteza Nove hronologije ipak ne „visi u vazduhu”, barem ne u potpunosti. Naime, Nosovski i Fomenko su, u slučaju drugog para cifara (5 i 6), priložili dosta „čvrstu” ilustraciju – graviru Albrehta Direra (Albrecht Dürer) pod nazivom Melanholija (vid. sl. 13). Prema zvaničnoj hronologiji gravira je datirana 1514. godinom, međutim, upravo imajući u vidu ovu „zamenu” cifara 5 i 6, Nova hronologija to datiranje dovodi u pitanje, i pretpostavlja da je reč o 1614. godini. Na pomenutoj graviri, u desnom gornjem uglu nalazi se magični kvadrat 4×4, kod koga su svi zbirovi (u svakoj koloni i svakom redu, kao i na dijagonalama) jednaki. Uostalom zato je i reč o magičnom kvadratu. Ali, kod ovog kvadrata ista suma (34) dobija se i kao zbir brojeva u „malom” kvadratu 2×2 koji se nalazi u središtu „velikog”, zatim kao zbir četiri broja u uglovima kvadrata, i najzad u sva četiri kvadrata na koja se deli „veliki”. Direrov magični kvadrat se smatra najranijim u evropskoj umetnosti, i istraživači ga nazivaju „kvadrat Jupitera”. Kao poseban kuriozitet ističe se da dva broja u sredini donjeg reda (15 i 14) pokazuju godinu nastanka kvadrata (odnosno, gravire).
Za nas je, međutim, važnije nešto drugo. Kako se jasno vidi na uveličanom fragmentu (sl. 14) brojka (cifra) 5 nalazi se na mestu gde je prvobitno bila upisana 6, i tragovi prepravljanja ne ostavljaju nikakvu sumnju. Kako je došlo do greške i zašto je Direr prvo upisao cifru 6? Naravno, tumači Direrovog dela davali su toj činjenici različitu interpretaciju i različit značaj. Po tumačenju Nove hronologije, međutim, to je rezultat okolnosti da se u vreme stvaranja gravire još nije ustalilo značenje novih, „arapskih” cifara 5 i 6, odnosno da je u početku cifra 6 imala „vrednost” 5.

Slika 15. Fragment gravire Bitka morskih bogova A. Direra
Izvor: G. V. Nosovskiй i A. T. Fomenko, Novaя hronologiя Rusi. Tom 2, Moskva, 2004, str. 239.
Sve to savremenom čitaocu može izgledati prilično čudno, i verovatno će mnogi nepoverljivo zavrteti glavom. Ipak, može se s velikom sigurnošću tvrditi da zapravo drugačije i nije moglo biti. Teško je, naime, zamisliti da su novi znakovi za cifre mogli da budu prihvaćeni kao konačni u momentu njihovog nastnaka. Bez obzira kako su nastali. Bio je, dakle, potreban određeni period u kom su one uspe(va)le da se nametnu, a u tom periodu same cifre morale su da prolaze kroz izvesne procese promena i prilagođavanja. Depmanova pretpostavka da nisu sve „arapske” cifre (u obliku u kojem ih mi danas poznajemo) nastale istovremeno potpuno je realna. Potvrđuju je ne samo ilustracije koje su u svojoj knjizi dali Nosovski i Fomenko, ilustracije koje prikazuju radove Direra, Kranaha, Friza. Na njima se vide „arapske” cifre vrlo čudnog (za nas) izgleda, koje, bar na prvi pogled, nije lako pročitati. Videti, na primer, sliku 15, na kojoj je zapisana godina, koja se zvanično čita kao 1494.

Slika 16. Istorija Fridriha i Maksimilijana, Altdorfer, 1510, fragment
Izvor: V. Višnёv. Strannыe datы.

Slika 17. Evolucija arapskih cifara od 12. do početka 16. veka
Izvor: E. Я. Gabovič, Istoriя pod znakom voprosa, Sankt-Peterburg, 2005, str. 352.
Zainteresovani čitalac može pronaći mnogo više takvih ilustracija u radu V. Višnjova[26], pri tome reč je ne samo datiranju u delima starih slikara, već recimo o predstavljanju cifara na starim časovnicima (na primer, slika 16). Sve to pokazuje (i dokazuje) da „arapske” cifre, u obliku u kojem ih mi poznajemo i koristimo, nisu nastale odjednom i istovremeno, već da je njihov nastanak i usvajanje (dugotrajan) proces tokom kojeg su se i one same menjale dok nisu konačno dobile sadašnji oblik. Iscrpne preglede te evolucije dao je Žorž Ifrah[27], a jedan od njih prikazan je na slici 17.
Savremeni desetni pozicioni brojčani sistem koristi se u značajnom delu sveta, pre svega u Evropi i Americi. Zasnovan na ciframa koje se nazivaju „arapskim” (ili „arapsko-indijskim”) on se danas, bar u zapadnom delu sveta, smatra univerzalnim, ali i „veoma starim”. Nastanak „arapskih” cifara smešta se u opšteprihvaćenoj istoriji u ne posle 5. veka, odakle su prenete u Evropu i tamo postale poznate u periodu 10-13 v. na osnovu (prevedenih) arapskih dela. Ovakva shvatanja danas preovlađuju, i pored toga što se bar u nekim autoritetnim enciklopedijskim izdanjima izražavaju tvrdnje da „do danas nemamo istorijski zasnovanu hipotezu koja bi dosta zadovoljavajuće objasnila poreklo naših cifara”.
Doista, upoznavanje s problemom nastanka „arapskih” cifara, makar i u dovoljno sažetom obliku, kako je to učinjeno u ovom radu, pokazuje da je reč o velikoj enigmi, kojoj se ne može i ne sme prilaziti površno i nenaučno. Njihov nastanak i širenje na teritoriju Evrope i zapadnog sveta moraju biti posmatrani kao istorijski proces tokom kog su se i sami te cifre menjale da bi konačno došle do sadašnjeg oblika. Ova velika zagonetka morala bi biti pogodno tle za istraživače raznih disciplina i raznih usmerenja. I to se tokom prethodnih vekova dešavalo, usled čega je i nastalo mnoštvo teorija i hipoteza, uključujući i neistorijske i nenaučne. One druge hipoteze i teorije, mada i (barem do sada) nedokazane, predstavljaju i treba da predstavljaju pogodan materijal za dalja istraživanja. To važi, naravno, i za nas i naše istraživače (istorije) nauke. Utoliko pre što se kod nas tokom prethodnih nekoliko godina (i čak decenija) pokušava s preispitivanjima prihvaće istorije (ili postavki „bečko-berlinske” istorijske škole).








