Један од најславнијих људи свог доба свакако је био италијански научник Ђироламо Kардано (1501–1576). Био је универзалист, радио је као математичар, физичар, лекар, астроном, астролог и професор на универзитетима у Павији, Милану и Болоњи. Међутим, због свог више него незгодног карактера, склон коцкању, свађама и подвалама, више пута хапшен, и данас важи за једног од најконтроверзнијих научника у историји.

Проф. др Миодраг Петковић
Ђироламо Kардано (1501-1576) био је један од најславнијих људи свог доба и мајстор многих вештина; радио је као математичар, физичар, астроном, лекар, астролог и професор на универзитетима у Павији, Милану и Болоњи. Истовремено, он је једна од најконтроверзнијих особа у историји науке.


Сл. 1 Ars Magna, Ђироламо Kардано (Wikipedia)
Kарданово најзначајније математичко дело Ars Magna (Велика вештина, штампано у Нирнбергу 1545), једна од најутицајнијих књига из области математике у 16. веку, садржи формулу за решавање кубне једначине, познату данас као Kарданова формула. Kубна једначина се најчешће посматра у облику
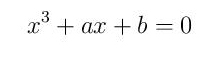
јер се општији облик
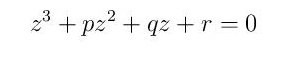
сменом
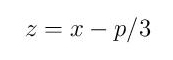
своди на разматрани облик
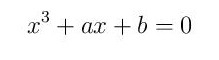
Тада су решења ове кубне једначине дата формулом
(1)
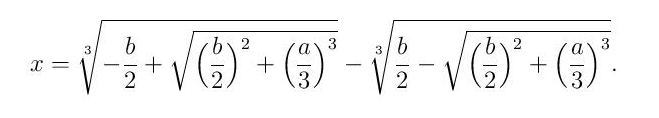
С обзиром да трећи корен има три вредности (гране), постоји 9 комбинација тако да избор три праве гране представља додатни проблем. Ову формулу је Kардано сазнао од другог великог италијанског математичара тог доба Николе Тартаље (право име Николо Фонтана, тартаља – муцавац) је надимак), тако да је због објављивања Тартаљиног резултата без његове сагласности у Kардановој књизи дошло до оштрог и мучног спора између ове двојице научника. Данас је познато да је до решења у општем облику први дошао Сципион дел Феро (1465-1526), неколико година пре Тартаље. Без обзира на ове чињенице формула (1) је нашироко позната као Kарданова формула (једна од његових већих превара) јер ју је он први описао у својој књизи Ars Magna (1545).
Описани пример „позајмице” туђег резултата само говори о томе колико је Kардано био контроверзна особа. Његов буран живот био је испуњен успесима и трагедијама, успонима и падовима, што га чини једним од најнеобичнијих карактера у историји математике и науке уопште јер је он био „мајстор свих заната”. Oн је био човек неочекиваних контраста. Упркос томе што се није могао похвалити „ни стасом ни гласом” због низа физичких мана, био je веома самоуверена особа која је на сваком месту, од кафана до краљевских дворова, наступала с позом „зар нисам најпаментнији”.
Шах и коцка су му биле велике страсти, при коцкању је први пут у историји користио неке елементе вероватноће, математичке области коју су нешто касније засновали Ферма и Паскал. Из коцкарских бурних свађа задобио је бројне ожиљке, а у једној прилици оптужен је за убиство. Такође је остало неразјашњено тровање његовог студента Лудовика Ферарија који је извео формулу за полиномску једначину четвртог степена користећи Фероов-Тартаљев-Kарданов метод.

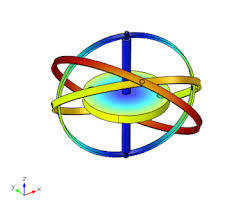
Сл. 2 Kарданов зглоб (спојница) и жироскоп (comsol.com)
Осим што је предавао медицину и математику, Kардано је писао радове из аритметике, астрономије, физике, механике, хидродинамике, геологије, и других области. Његово главно дело Ars Magna (1545) је прва велика студија на латинском језику посвећена искључиво алгебра, где се први пут помињу негативни бројеви. Вероватно су многи читаоци чули за карданов зглоб који се користи код аутомобила и других машина за трансмисију (ротационе) погонске силе, али је вероватно да врло мали број људи зна да је то изум Ђиролама Kардана. Осим тога, конструисао је механизам који се састојао од три концентрична прстена који слободно ротирају око осе, што је представљало претечу жироскопа.
На врхунцу славе Ђироламо Kардано важио је за водећег светског научника свог времена. Према чувеном историчару математике Е. Т. Белу, он је више пута одбијен да буде именован за професора на универзитету у Милану, да би се напослетку вратио као ректор! Био је, такође, чувени лекар (посао којим се бавио илегално), чија је добра репутација далеко превазишла овај град јер је био познат у целој Европи. Године 1552. прихватио је позив да помогне Џону Хамилтону, шкотском надбискупу, који је патио од тешких напада астме. Врло брзо је закључио да су ови напади узроковани јаком алергијом на перје, па је захтевао да се надбискупов јастук замени. Након уклањања извора, надбискупово здравље се моментално побољшало, а Kардано је истовремено постао и веома славан и веома богат.
Био је мање успешан када се прихватио да сачини хороскоп младог шеснаестогодишњег краља Енглеске, Едварда Шестог (сина краља Хенрика Осмог и Џејн Сејмор, описан на посредан начин у књизи Kраљевић и просјак Марка Твена). Предвидео му је дуг и срећан живот али је, нажалост, краљ умро пре него што се Kардано вратио кући из Енглеске.
Године 1570. године доспео је у тамницу у којој је провео неко време. Ухапшен је јер је његова екстравагантна идеја да направи хороскоп Исуса Христа протумачена од стране цркве као јерес. Напустивши катедру на Универзитету у Болоњи, прешао је у Рим где је постао истакнити астролог и добијао пензију од папе. Умро је у Риму 1576. године под неразјашњеним околностима, што и није било баш необично јер је због свог незгодног карактера имао велики број непријатеља, од уличних разбојника и коцкара, до самог папе.
Kратка прича довољно говори да је Ђироламо Кардано био универзалан научник немирног духа. Зато није никакво чудо што се бавио и играчкама чије решење има математички карактер. Једна од најпознатијих је веома распрострањена играчка, позната као кинески прстенови на слици 3. Французи зову ову играчку La Baguenodier (играчка с колутовима), а Енглези је зову The Tiring Irons (умарајући окови). Мада врло старог порекла, она се и данас продаје широм света. Упркос своме имена, њено наводно кинеско порекло није доказано до данашњих дана; Ђироламо Kардано је био први који је описао ову играчку-загонетку 1550. године у делу De Subtilitate. Kасније се ова загонетка успут помиње у 7. глави романа Hongloumeng (Сан црвене дворане) из 1791. Такође ју је разматрао енглески математичар и свештеник Џон Волис (1616-1703) у својој Алгебри (издање на латинском, 1693).
Играчка-загонетка кинески прстенови састоји се од извесног броја прстенова окачених на дугу жичану петљу на такав начин да је она обухваћена прстеновима у почетном положају (слика 3). Сваки прстен је лабаво повезан помоћу малог вертикалног држача за платформу испод петље. Осим последњег (најудаљенијег од краја петље), сваки од везних држача је обухваћен одговарајућим прстеном да би се спречило извлачење прстена из петље. Прстен може да клизи дуж петље до њеног краја и може се скинути с петље једино ако су сви прстенови од посматраног прстена до краја петље већ скинути. Стављање на петљу одвија се обратним редом. Поредак прстенова се не сме мењати. Задатак се састоји у скидању свих прстенова са петље у минималном броју потеза.
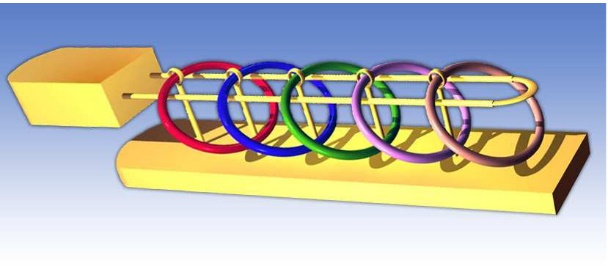
Сл. 3 Kинески прстенови (Владимир Петковић)

Сл. 4 Ханојска кула (Владимир Петковић)
Слично као у случају добро познате ханојске куле (слика 4), при решавању загонетке кинески прстенови неопходна је примена инверзног поступка (враћање прстенова натраг на петљу). Ова рекурзивна особина тесно повезује поменуте две загонетке. Штавише, изванредно лепе идеје (у оба случаја засноване на коришћењу бинарног бројног система) при решавању чине их веома сличним. Загонетки кинески прстенови посвећена је обимна литература која се састоји од неколико књига и стотинак научних радова. Поступак за налажење укупног (минималног) броја корака, неопходних за извлачење свих н прстенова са петље, описали су Рауз Бол и Kоксетер у књизи Mathematical Recreations and Essays (Dover Publication, Њујорк 1987). Минимални број потеза је
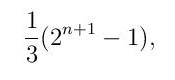
ако је n непарно и
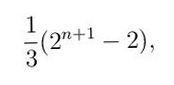
ако је n парно.
Напоменимо да Ђироламо Kардано и Џон Волис нису нашли оптималан поступак за решавање загонетке с прстеновима (самим тим, нису ни знали минималан број потеза). Елегантно решење дао је француски математичар Луј Гро (Louis Gros) у студији Thèorie du Baguenodier (Лион, 1872). Његов приступ решавању се може сматрати претечом тзв. Грејових кодова, названих тако по инжењеру Френку Греју (Frank Gray), запосленом у компанији AT&T Bell Laboratories, који је радио на развоју технике (де)кодирања и корекције грешке тридесетих година двадесетог века. Подсетимо да је француски инжењер Емил Бодо користио ову врсту кодова у телеграфији 1878. године, знатно пре Греја.
Френк Греј је изумео метод за конверзију аналогног сигнала у бинарни Грејов код користећи вакуумске цеви. Данас Грејови кодови имају значајну примену у теорији графова и теорији бројева, а користе се и у корекцији грешака у дигиталним комуникацијама, као што је трансмисија ТВ сигнала, и да учине трансмисију система мање осетљивом на шумове. Њихово генерисање дато је у табели 1.
У табели 1 приказани су децимални бројеви од 0 до 21 у бинарној репрезентацији (са основом 2). Овим бинарним бројевима генерисани су Греј-код бинарни бројеви. Сваки петоцифрени Греј-код број се добија из одговарајућег бинарног броја на основу следећег правила: рачунајући бинарне бројеве слева на десно, прва Греј-код цифра је увек једнака првој цифри бинарног броја. После тога, свака Греј-код цифра је 1 ако се одговарајућа бинарна цифра разликује од своје претходне (посматрајући улево); у супротном, ова цифра је 0.
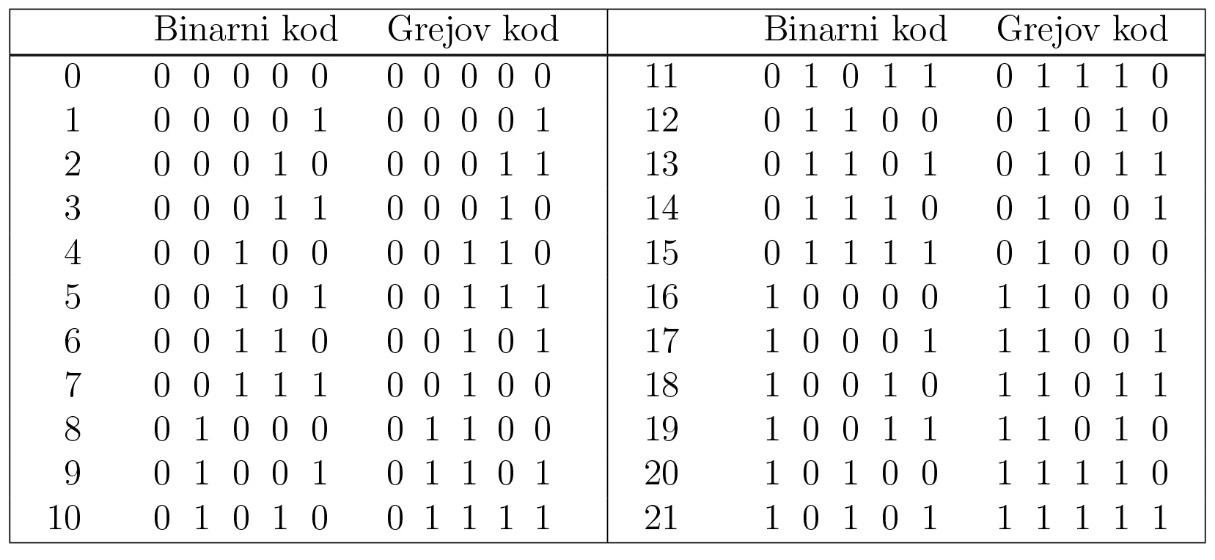
Табела 1 Бинарни бројеви и Греј-код бројеви
У наставку ћемо изложити део процеса за решавање загонетке са 5 прстенова засновано на бинарним и Греј-код бројевима. На основу претходног, следи да оптимално решење захтева (2^6-1)/3=21 потез. Свака позиција прстена се представља помоћу Грејовог петоцифреног бинарног низа нула и јединица, при чему прстену на петљи одговара 1, а прстену ван петље 0. Последња цифра одговара позицији првог прстена (најближег крају петље), док прва цифра одговара позицији петог прстена. Илустрације ради, дајемо неколико позиција прстенова и одговарајуће Грејове (петоцифрене) бинарне бројеве:
1 1 1 1 1 (сви прстенови су на петљи),
1 0 1 1 1 (четврти прстен је ван петље),
1 1 0 1 0 (први и трећи прстен су скинути),
0 0 0 1 1 (први и други прстен су на петљи),
0 0 0 0 0 (сви прстенови су скинути).
На велико изненађење, постоји невероватна коинциденција између Греј-код бинарних бројева и решења загонетке с прстеновима: у обратном редоследу (од 21 до 0 у случају пет прстенова) Греј-код бројеви управо показују сукцесивне позиције прстенова у траженом минималном решењу, при чему први Греј-код број 11111 показује почетни положај (сви прстенови су на петљи). На основу табеле 1 можемо направити шему (приказану на слици 5) која сликовито приказује прве потезе потребне да би се скинула три прстена са петље. Придружени Греј-код бројеви приказују сукцесивне позиције прстенова, представљених малим кружићима.
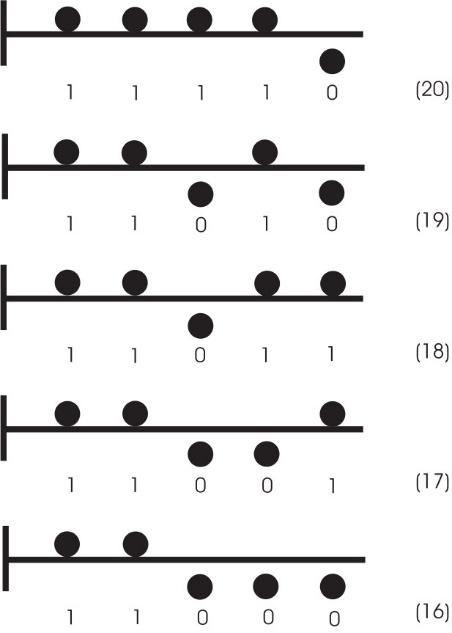
Сл. 5 Пет прстенова и одговарајући Греј-код бројеви








