Интересантно је да назив Хамилтонов пут потиче од игре на додекаедру (правилни полигон који има 12 страна-правилних петоуглова, 20 темена и 30 ивица, сл. 3) који је поставио већ поменути ирски математичар Вилијам Хамилтон. Игра се продавала под именом icosian (icosa – на грчком двадесет) или Пут око света.

Проф. др Миодраг Петковић
Повремено ће се у овој рубрици у Галаксији појављивати занимљиви прилози из света математике који укључују интересантне формуле, догађаје из света математике и живота великих математичара и елементарне али интригантне и изазовне задатке за чије решавање је довољно средњошколско знање математике. Већина ових прилога, и још математичких прича и занимљивости може се наћи на сајту www.miodragpetkovic.com, аутора ових прилога (опција теме у менију).
Трговац планира да обиђе све градове у неком региону (држави или и шире) али тако да у сваки град сврати једном и само једном. И ако је могуће, да се врати у полазно место. Било би најбоље да укупун пут буде најкраћи могући. Овако једноставан (?!) план довео је до једног од најтежих проблема у математици, а како изгледа према савременим познавањима физике, проблем се не може решити у општем случају. У литертури он познат као „Проблем трговачког путника” (Travelling Salesman Problem, скраћено TSP) и на ову тему написано је више хиљада и научних радова и књига.
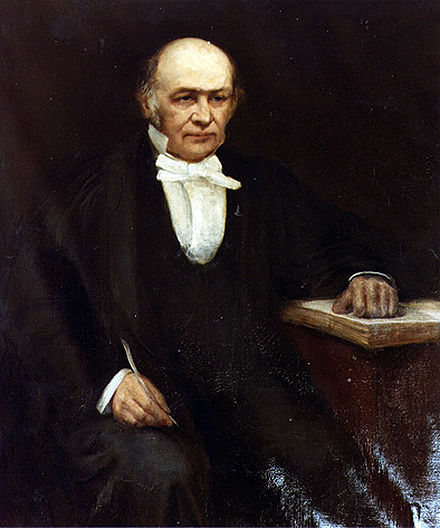
Вилијам Роуван Хамилтон (Wikipedia)
Математички прилаз први је дао у првој половини 19. века Вилијам Роуан Хамилтон (1805-1865, Даблин, Ирска), један од највећих математичара 19. века, чије име носе неколико појмова и назива у механици и математици. Проблем је од огромног практичног значаја и отуда велико интересовање за налажење бар приближног решења, што је нарочито постало актуелно са развојем брзих рачунара, праћено креирањем веома ефикасних алгоритама.
Математички посматрано, проблем се може описати на следећи једноставан начин. Нека је у равни задат коначан скуп од n непреклапајућих тачака А1,…Аn (сл. 1). Jедан од најважнијих математичких проблема, како са теоријског, тако и са практичног становишта, гласи: Обићи све тачке А1,…Аn mреже пролазећи кроз сваку тачку једном и само једном.
Путеви код којих је могућ овакав обилазак зову се Хамилтонови путеви. Затворен Хамилтонов пут који се завршава у почетној тачки зове се Хамилтонова контура. Хамилтонов пут за конфигурацију са слике 1 приказан је на слици 2. Ово је и Хамилтонова контура, јер је могуће из последње тачке A9 доћи у полазну тачку A1
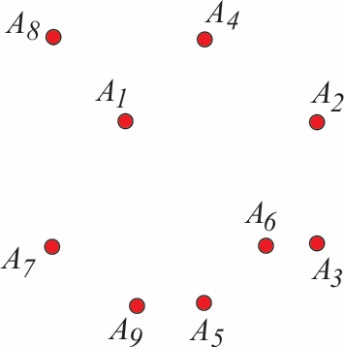
Сл. 1 Да ли постоји Хамилтонов пут?
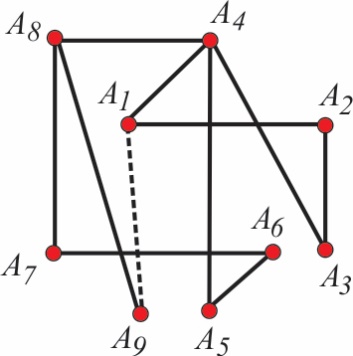
Сл. 2 Хамилтонов пут за конфигурацију са слике 1
Тачке са слике 1 могу бити градови, аеродроми, чворови у архитектури микропроцесора, војне базе итд. Одавде је прилично јасно зашто су Хамилтонови путеви од великог интереса у многим применама, као што су телекомуникационе мреже, авио-саобраћај, транспорт, дизајнирање микропроцесора, разне логистике. Општи алгоритам (једноставан или компликован) за налажење Хамилтонових путева још увек није смишљен, и то је један од најтежих али и најважнијих нерешених проблема у теорији графова, теорији оптимизације, теорији рачунарских наука и, генералније, у читавој математици. Проблем се екстремно компликује ако се тражи пут минималне дужине, тј. минимум суме
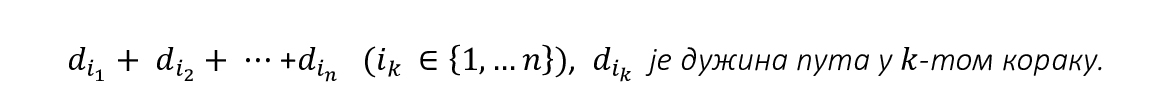
Дакле, овде имамо два проблема: 1) потребно је најпре наћи све Хамилтонове путеве (ако уопште постоје, и ако постоје, одредити их) и 2) одредити Хамилтонов пут минималне дужине. Уместо минималне дужине, као критеријум се може задати и минимално утрошено време пута, најнижи трошкова пута и слично.
Чак и ако број објеката n није велики (рецимо 100), ни данашњи суперрачунари не могу егзактно да реше овај проблем јер време извршења расте више него експоненцијално, отприлике реда n! gde n! означава производ свих природних бројева од 1 па закључно до n. Рецимо, 4!=24, 10! =3 628 800, a 50! је број који се пише са 64 цифре. Замислите проблем оптималног авио-саобраћаја у САД која има око 5.000 цивилних аеродрома. Још 1995. године једна велика америчка авио-компанија понудила је награду од 20 милиона долара за скоро оптимално решење (није баш сасвим јасно шта се под тим подразумевало). Награду није нико добио.
У броју 3/2020 штампаног издања „Галаксије” професор Мирко Вујошевић је у чланку „Аријаднин траг” опширно писао о TSP. Наглашено да TSP припада групи најтежих оптимизационих проблема за који се ни изблиза не назире решење у општем случају, а експерти верују да ни рачунари милијарду милијарди пута бржи од данашњих супер рачунара не могу да реше сваку конфигурацију јер ни време мерено милијардама година није довољно.
Интересантно је да назив Хамилтонов пут потиче од игре на додекаедру (правилни полигон који има 12 страна-правилних петоуглова, 20 темена и 30 ивица, сл. 3) који је поставио већ поменути ирски математичар Вилијам Хамилтон. Игра се продавала под именом icosian (icosa – на грчком двадесет) или Пут око света.
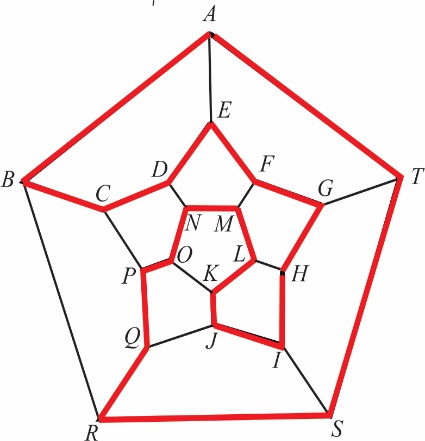
Наћи пут по ивицама додекаедра који кроз свако теме додекаедра пролази једном и само једном. До решења се лако долази ако се додекаедар представи преко своје стереографске пројекције у равни, тзв. скелетона додекаедра. Једна Хамилтонова контура дуж скелетона приказана је на слици 9 помоћу подебљаних линија у црвеној боји.
Сл. 3 додекаедар
Сл. 4 Хамилтонова контура
Поменули смо да је Хамилтонов пут на додекаедру често популарно описиван као Пут око света. Користећи моћни програмски пакет Mathematica који је осмислила (и даље усавршава) компанија Wolfram (на челу са идејним творцем Стивеном Волфрамом), могуће је направити симулацију Пута око света, при чему се заиста обилазе главни градови свих држава света (по контури која апроксимира Хамилтонову). При овоме се користи база CountryData коју поседује овај софтвер и апликација Graphics3D за цртање. Скица путање може се видети на Волфрамовом линку:
Ево још једног чувеног примера (из арапских списа, 9. век) из рекреативне математике: Пут који шаховска фигура скакач направи на стандардноj шаховској табли 8 x 8 тако да обиђе сва 64 поља, прелазећи преко сваког поља једном и само једном, и притом се враћа на полазно поље, чини Хамилтонову контуру.
Овим проблемом бавили су се чувени математичари Ојлер, Вандермонд, Лежандр, Де Муавр, Де Монмор и други. На слици 5 приказано је Ојлерово решење из 1757. (у време када је био потпуно слеп).
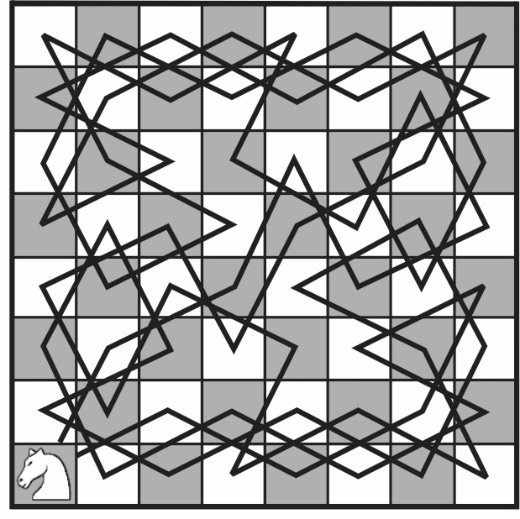
Сл. 5 Ојлерово решење скакачеве
Хамилтонове контуре
Додајмо на крају интересанту причу о Хамилтоновом опредељењу за математику. Као дечака, ујак лингвиста га је усмеравао на учење страних језика. Хамилтон је био чудо од детета: у петој години читао је књиге на грчком и хебрејском језику; такође је могао да пише на француском и италијанском; у десетој је учио арапски и санскрит; у дванаестој већ је добро знао ове језике, заједно са сиријским, персијским, хинду и малајским.
Прекретница у његовом животу настала је када је имао дванаест година, после сусрета са америчким „живим калкулатором” Зиром Колберном. Зира Колберн је могао да изводи напамет компликована аритметичка израчунавања и Хамилтон је одлучио да опроба своје способности у такмичењу са њим. Испоставило се да је пораз од Колберна пробудио код Хамилтона велики интерес за математику, којој се одмах после тога потпуно посветио.








