У овом кратком прилогу бавимо се темама у вези са непрекидним функцијама и њеним особинама. Разматрана је тзв. Палачинка теорема, а затим два једноставна задатка, температуре на екваторској линији и пут планинара. Условно речено једноставни јер решења захтевају суптилне идеје. Оба задатка су често саставни део тестирања у ИТ компанијама.

Проф. др Миодраг Петковић
Из математичке анализе добро је познато тврђење.
Теорема 1. Ако непрекидна крива дефинисана једначином y = f(x) има минималну вредност А и максималну вредност B на интервалу дефинисаности [а,b], тада функција f мора узети сваку вредност између А и B.
Ово тврђење је интуитивно јасно на основу графика функције f на [а,b], слика 1. У овом прилогу употребићемо теорему 1 да докажемо један интересантан резултат у литератури познат и као палачинка теорема.
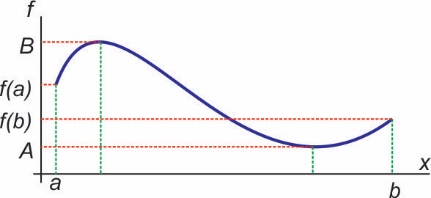
Сл. 1 Непрекидна функција (уз теорему 1)
Подела затворене раванске области
Посматрајмо област у равни ограничену затвореном линијом која не сече саму себе. То може да изгледа као палачинка (сл. 2) па отуда и назив горе поменуте теореме. Питање гласи: Да ли се ова област може поделити правом на два дела једнаких површина и то полазећи из било ког правца?
Одговор је позитиван: може. Да бисмо то доказали, најпре повуцимо праву X изван области (палачинке) F под произвољним углом (овим је дефинисан произвољан правац поменут у задатку), видети слику 2. Нека је површина области F једнака PF.
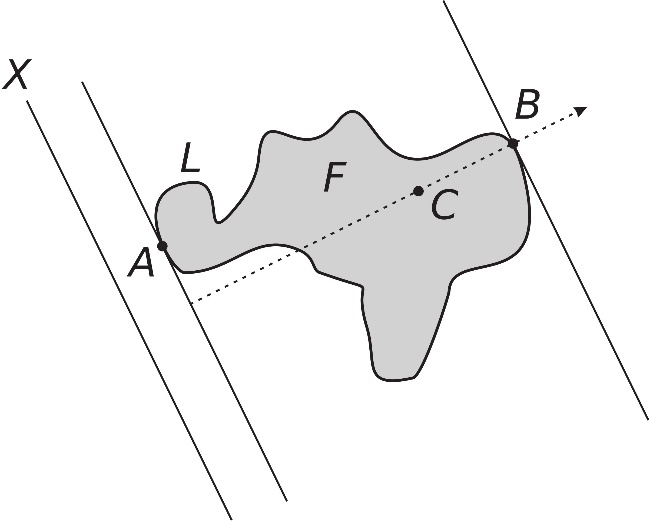
Сл. 2 Палачинка теорема
Означимо са PF(C) површину исечену од фигуре F правом која пролази кроз унутрашњу тачку C (сл. 2). Померајмо праву X према граничној контури L области F задржавајући исти угао све док X не додирне линију L у тачки А. У овој стартној позицији ниједан део фигуре F није покривен, према томе имамо да је PF(A) = 0. Права X затим наставља од тачке А да сече фигуру F. Јасно је да у тачкама C унутар области F важи PF(C) > 0. Права X излази из области F у тачки B, тада је област F потпуно прекривена и имамо да је PF(B)=PF. Вредност PF(C) непрекидно расте док се права X помера од улазне тачке А до излазне тачке B узимајући све вредности од 0 до PF. На основу теореме 1 са почетка текста, у једној позицији тачке C* мора бити PF(C*) = PF/2, што потврђује да постоји решење постављеног задатка. Овим смо доказали палачинка теорему.
Теорема 2. Област у равни ограничена затвореном линијом која не сече саму себе може се поделити правом на два дела једнаких површина и то полазећи из било ког правца.
Штавише, на основу доказа горње теореме следи да се од области F увек може одрезати област чија је површина једнака n-том делу површине области F јер у некој тачки C** биће PF(C**) = PF/2. Приметимо да изложена дискусија не даје одговор о позицији тачке C*.
Температура на екватору
Следећи интересантан задатак се решава користећи управо изложен концепт непрекидности. Доказати да на екваторској линији постоје две дијаметрално супротне тачке у којима су температуре једнаке.
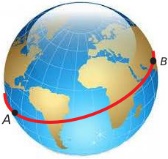
Сл. 3 Температура на екватору
Решење: Посматрајмо на екватору међусобно супротне тачке А и B у којима је температура редом ТА и ТB, слика 3. Без губљења општости можемо да претпоставимо да разлика ТА-ТB има позитивну вредност. Пустимо сада да тачке А и B ротирају истовремено по екваторској линији задржавајући њихову опозицију, све док не замене места. Температуре ТА и ТB тачака А и B се све то време мењају и у новом положају имамо да је ТА-ТB < 0 јер тачка А је заузела место тачке B (која је хладнија). С обзиром да је разлика ТА-ТB од позитивне вредности (пре почетка кретања по екваторској линији) постала негативна после завршеног полукружног кретања, због континуалне промене температурне разлике, у неком моменту ова разлика је морала да буде једнака нули. Тај моменат одређује позиције супротних тачка на екватору у којима је температура једнака.
Планинаров пут
Kористећи исти принцип, може се решити и следећи интересантан задатак који је задавао муке и универзитетским професорима иако је решење врло једноставно – наравно, ако се има права идеја: Једног дана, тачно у 6 ујутру, планинар је почео да се пење уском стазом која је спирално водила до планинарског дома на врху планине. Планинар је ишао неравномерном брзином, често се одмарајући на свом путу. На врх планине стигао је пред залазак сунца. Пошто је преспавао у планинарском дому, сутрадан ујутру је у 6 сати кренуо низ планину. Спуштао се истом стазом и ишао неравномерним кораком, повремено се одмарајући. Доказати да постоји тачка на стази у коју ће он доспети приликом спуштања тачно у исто време као и претходног дана док се пењао уз планину.
За решавање овог задатка није потребно никакво математичко знање. Пре излагања решења за нестрпљиве читаоце дајемо паузу за освежење у виду лепог планинског пејзажа. Они упорнији могу да запосле свој мозак тражећи идеју за решавање заустављајући се код доње слике. Решење садржи врло једноставну али и ефектну идеју и поново је засновано на принципу континуитета.

(Владимир Петковић)
Решење: Претпоставимо да у планинарењу учествују два планинара: један који је у 6 ујутру почео да се пење уз планину, и други који је у исто време и истом стазом почео да се спушта низ планину. У неком моменту они се морају срести на стази; тачка сусрета је управо тражена тачка јер је од времена поласка обојице планинара протекло исто време.








