Математичка оптимизација је поступак избора најбољег елемента из скупа доступних алтернатива који задовољава одређене услове. Проблеми оптимизације се јављају у бројним квантитативним дисциплинама, од рачунарских наука и инжењерства до операционих истраживања и економије. Због тога се овој области примењене математике вековима посвећује велика пажња. Описаћемо Херонов принцип минимума (1. век) који има историјски значај јер га сматрају првом студијом неког оптимизационог проблема.

Проф. др Миодраг Петковић
Херон из Александрије је вероватно рођен у Александрији (данас другом по величини граду у Египту) око 10. године нове ере. а умро је око 75. године. Остао је упамћен по бројним изумима као што су Херонова фонтана (водена прскалица која се и данас често користи за наводнавање травњака), примитивном прототипу парне машине и бројним проналазцима из пнеуматике, оптике, механике, геометрије и мерења површина, тако да се може сматрати првим инжењером у историји са Архимедом. Средњошколцима је сигурно познат по формули за израчунавање површине троугла са страницама a, b i c:
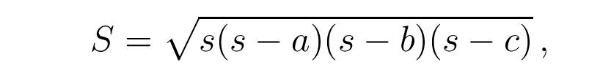
где je s = (a + b + c)/2 полуобим троугла.

Херон
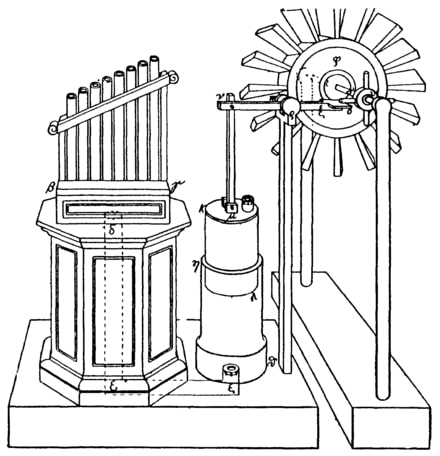
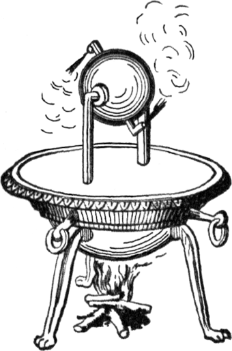
Херонови изуми (Wikipedia)
Kористећи једноставне геометријске аргументе, он је демонстрирао је закон рефлексије (познат раније Архимеду и Аристотелу) у својем делу Рефлексија
(Catoptrica). Показао је да пут зрака светлости од извора, преко рефлектујућег огледала до ока посматрача мора бити што је могуће краћи. Херон је посматрао следећи проблем који се данас може наћи у скоро сваком уџбенику из геометрије: А и B су две дате тачке са исте стране праве k. Одредити тачку C на правој k тако да сума растојања од А до C и од C до B буде минимална.
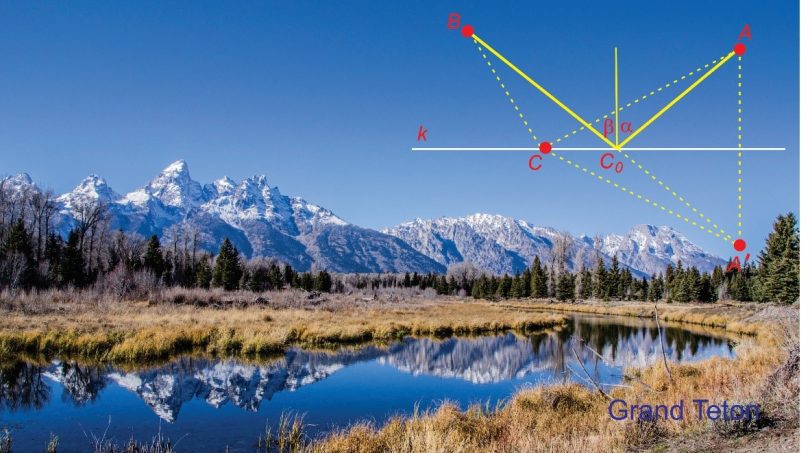
Геометријско решење Хероновог проблема се лако изводи помоћу слике 1.
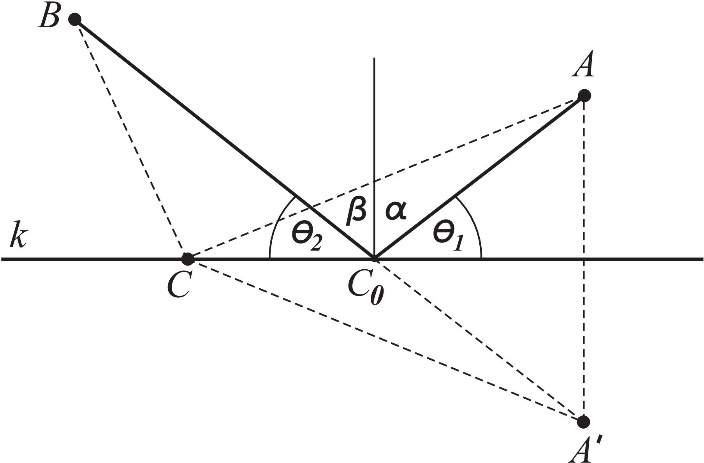
Слика 1
Нека је А’ тачка симетрична тачки А у односу на праву k и нека је C произвољна тачка на правој k. Спојимо B са А’ и означимо са C0 тачку пресека дужи BА’ и праве k. Нека |СТ| означава дужину дужи СТ. Kако је троугао CАА’ равнокрак, имамо
![]()
Због тога је
![]()
где једнакост важи ако и само ако се тачка C поклапа са C0.
Последња релација даје решење проблема. Тражена тачка која обезбеђује минималну суму траженог растојања је пресек дате праве k и дужи чији су крајеви дата тачка B и тачка А’ симетрична другој датој тачки А у односу на праву k.
У својој књизи О огледалу Херон је размотрио физичку ситуацију из које проистиче горњи задатак. Нека је А извор светлости, тачка B пријемник светлости (нпр. око посматрача), а права k пресек равни у којој се налазе тачке B и А и на њу управне равни огледала, која служи као рефлектујућа површина. Зрак светлости који долази после одбијања у пријемник B привидно стижеи из тачке А’ симетричне тачки А у односу на праву k (лик у огледалу). Одавде следи да је упадни угао α једнак одбојном углу β (видети слику 1).
Из горњег разматрања Херон је закључио да се зрак светлости рефлектује од огледала на такав начин да је његова путања између извора светлости и пријемника светлости најкраће могуће дужине. Ова особина је, у ствари, Фермаов принцип минималног времена или закон одбијања светлости који је пре њега експериментално утемељио холандски физичар и математичар Вилеброрд Снел (1580–1626). Херонов проблем и његово решење имају своје место у историји јер је то био први пример примене принципа минимума у описивању физичких појава.
Напоменимо да неки модерни уџбеници описују проблем кроз различите практичне проблеме. На пример, права k се узима за железничку пругу док тачке А и B постају градови, тачка C је будућа железничка станица коју треба саградити, а питање гласи: Где треба градити железничку станицу тако да је укупна дужина путева којима су градови спојени са станицом најкраћа?

(Sunset Train, Владимир Петковић)
У вези са описиваним дајемо занимљив геодезијски проблем који је поставио највећи енглески састављач занимљивих проблема и загонетки Хенри Дудени (1857–1931) у својој књизи Modern Puzzles (Лондон, 1926): На спољашњој страни чаше цилиндричног облика (отвореној горе) у тачки А налази се мува, а на унутрашњој страни у тачки B кап меда. Kојим путем треба да иде мува да би што пре стигла до меда? Подразумева се да мува не лети до меда већ иде по површинама чаше (спољној до ивице а затим по унутрашњој), као и да је дебљина чаше занемарљива.
Означимо позиције муве и меда тачкама А и B. Ако ове две тачке леже на истој изводници ваљка, решење је очигледно те ћемо надаље претпоставити да то није случај. Развијени омотач ваљка даје правоугаоник (слика 4а).
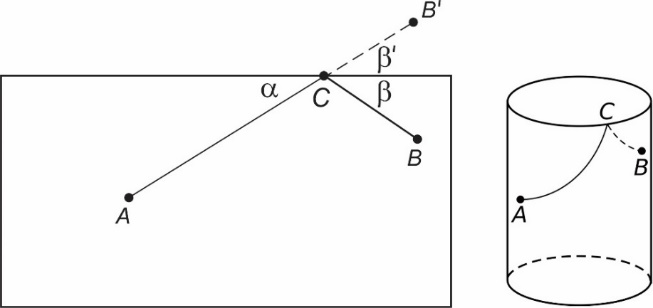
а) b)
Слика 4 Мува и кап меда
Проблем се сада своди на одређивање најкраћег пута АCB, где је C тачка на ивици чаше. У ствари, ово је Херонов проблем и решење користи симетричну тачку B’ тачке B у односу на ивицу часе. Упадни угао α једнак је одбојном углу β (= β’). Мува ће пузити по површини часе дуж два лука цилиндричне спирале (слика 4b), прелазећи преко ивице чаше у тачки C.
Херонов принцип се, такође, може успешно применити за налажење најкраћег пута у следећој ситуацији описаној у неколико књига на руском и енглеском језику. Аутор овог прилога уврстио је овај задатак у своју књигу Famous Puzzles of Great Mathematics (American Mathematical Society, 2009), која припада и историји математике и рекреативној математици.
Жељан одмора од буке велеграда и шпанских, индијских и турских ТВ серија, млади авантуриста отишао је на одмор у Африку. После краћег лутања пронашао је дивно место на ушћу двеју река које су правиле полуострво у облику оштрог угла (сл. 5). Сваког дана авантуриста напушта своју колибу (C), иде до једне обале (А) полуострва да посматра ватерполо-меч између локалних племена, затим иде до друге обале (B) да бере лотосове цветове и евентуално помилује свог омиљеног нилског коња, а потом се враћа у колибу. Ове његове шетње иду приближно истом трасом, али нису и најкраће. Kоји пут он треба да изабере да би укупан пут CABC био најкраћи?

Слика 5 Авантуриста на полуострву (Владимир Петковић)
Нека полуправе pА и pB означавају обале река и нека је са C означена позиција колибе. Нека су CA и CB тачке симетричне тачки C у односу на полуправе pA и pB (сл. 6).
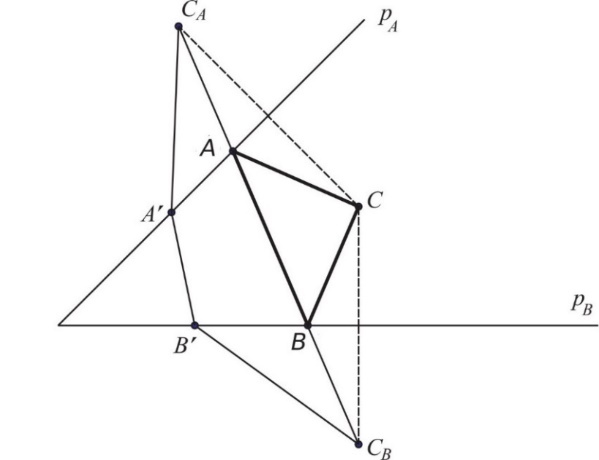
Слика 6 Авантуриста на полуострву – решење
Спојимо тачке CА и CB и означимо са А и B пресечне тачке дужи CACB и полуправих pA и pB. Пресечне тачке А и B одређују места на обалама река која обезбеђују најкраћи пут CACB авантуристе. Заиста, ако су А’ и B’ произвољне тачке на pA и pB, тада је
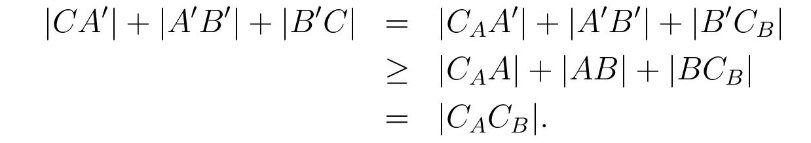
Другим речима, најкраћи пут између тачака CA и CB иде дуж праве линије. Пресечне тачке А и B одређују места на обалама до којих авантуриста треба да трасира свој најкраћи пут.
Херонов проблем био је вековима инспирација математичарима да постављају сличне и изводе разне генерализације. Поменућемо на крају само један довољно једноставан да заинтересује аматере за самостално решавање. Славни математичар Пјер де Ферма (1601–1665) (узгред, био је правник који си у слободном времену бавио математиком) почетком 17. века на крају својег чувеног есеја о оптимизационим проблемима поставио је следећи задатак: У равни су дате три тачке А, B и C такo да троугао АBC нема угао већи од 120 степени. Одредити четврту тачку Т тако да је збир њених растојања до три дате тачке минималан. Дакле, треба одредити позицију тачке Т у равни тачака А, B и C тако да је сума |ТА + ТB + ТC| што је могуће мања.
Фермаов проблем скренуо је пажњу еминентном италијанском математичару и физичару Евангелисти Торичелију (1608–1647) који је око 1640. описао геометријску конструкцију за његово решење. Kасније је написано више научних радова у којима је дато неколико генерализација Хероновог проблема. Ови резултати, а и Торичелијево решење, могу се наћи у: Јакоб Kраруп, On Torricelli’s geometrical solution to a problem of Fermat, IMA Journal of Mathematics Applied in Business and Industry (1997) 8, 215-224. Заинтересованим читаоцима могу послати копију у pdf-у, моја адреса је miodragpetkovic@gmail.com са назнаком Kраруп.
(Илустрација Гранд Тетон, Вајоминг, САД/Миодраг Петковић