Matematička optimizacija je postupak izbora najboljeg elementa iz skupa dostupnih alternativa koji zadovoljava određene uslove. Problemi optimizacije se javljaju u brojnim kvantitativnim disciplinama, od računarskih nauka i inženjerstva do operacionih istraživanja i ekonomije. Zbog toga se ovoj oblasti primenjene matematike vekovima posvećuje velika pažnja. Opisaćemo Heronov princip minimuma (1. vek) koji ima istorijski značaj jer ga smatraju prvom studijom nekog optimizacionog problema.

Prof. dr Miodrag Petković
Heron iz Aleksandrije je verovatno rođen u Aleksandriji (danas drugom po veličini gradu u Egiptu) oko 10. godine nove ere. a umro je oko 75. godine. Ostao je upamćen po brojnim izumima kao što su Heronova fontana (vodena prskalica koja se i danas često koristi za navodnavanje travnjaka), primitivnom prototipu parne mašine i brojnim pronalazcima iz pneumatike, optike, mehanike, geometrije i merenja površina, tako da se može smatrati prvim inženjerom u istoriji sa Arhimedom. Srednjoškolcima je sigurno poznat po formuli za izračunavanje površine trougla sa stranicama a, b i c:
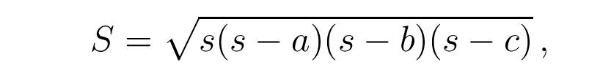
gde je s = (a + b + c)/2 poluobim trougla.

Heron
Heronovi izumi (Wikipedia)
Koristeći jednostavne geometrijske argumente, on je demonstrirao je zakon refleksije (poznat ranije Arhimedu i Aristotelu) u svojem delu Refleksija
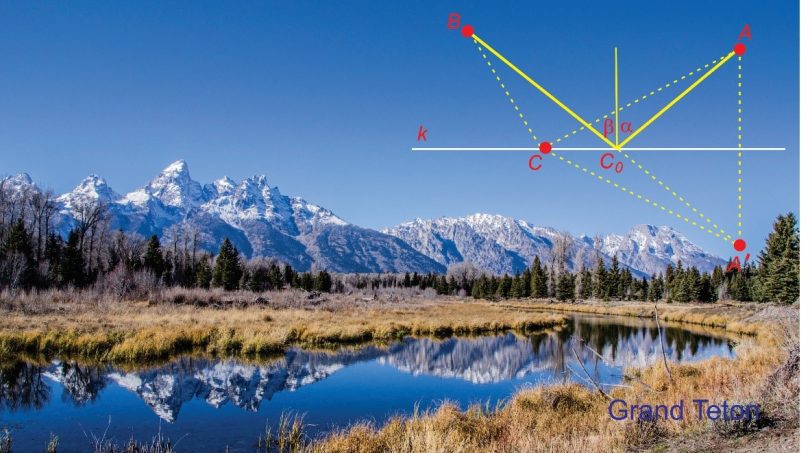
(Catoptrica). Pokazao je da put zraka svetlosti od izvora, preko reflektujućeg ogledala do oka posmatrača mora biti što je moguće kraći. Heron je posmatrao sledeći problem koji se danas može naći u skoro svakom udžbeniku iz geometrije: A i B su dve date tačke sa iste strane prave k. Odrediti tačku C na pravoj k tako da suma rastojanja od A do C i od C do B bude minimalna.
Geometrijsko rešenje Heronovog problema se lako izvodi pomoću slike 1.
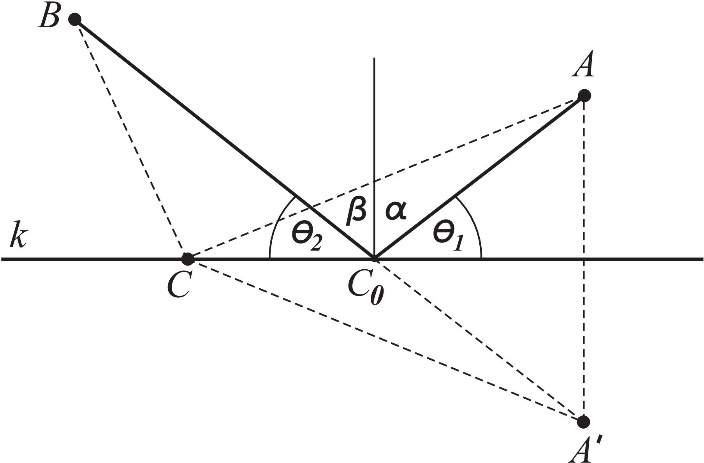
Slika 1
Neka je A’ tačka simetrična tački A u odnosu na pravu k i neka je C proizvoljna tačka na pravoj k. Spojimo B sa A’ i označimo sa C0 tačku preseka duži BA’ i prave k. Neka |ST| označava dužinu duži ST. Kako je trougao CAA’ ravnokrak, imamo
![]()
Zbog toga je
![]()
gde jednakost važi ako i samo ako se tačka C poklapa sa C0.
Poslednja relacija daje rešenje problema. Tražena tačka koja obezbeđuje minimalnu sumu traženog rastojanja je presek date prave k i duži čiji su krajevi data tačka B i tačka A’ simetrična drugoj datoj tački A u odnosu na pravu k.
U svojoj knjizi O ogledalu Heron je razmotrio fizičku situaciju iz koje proističe gornji zadatak. Neka je A izvor svetlosti, tačka B prijemnik svetlosti (npr. oko posmatrača), a prava k presek ravni u kojoj se nalaze tačke B i A i na nju upravne ravni ogledala, koja služi kao reflektujuća površina. Zrak svetlosti koji dolazi posle odbijanja u prijemnik B prividno stižei iz tačke A’ simetrične tački A u odnosu na pravu k (lik u ogledalu). Odavde sledi da je upadni ugao α jednak odbojnom uglu β (videti sliku 1).
Iz gornjeg razmatranja Heron je zaključio da se zrak svetlosti reflektuje od ogledala na takav način da je njegova putanja između izvora svetlosti i prijemnika svetlosti najkraće moguće dužine. Ova osobina je, u stvari, Fermaov princip minimalnog vremena ili zakon odbijanja svetlosti koji je pre njega eksperimentalno utemeljio holandski fizičar i matematičar Vilebrord Snel (1580–1626). Heronov problem i njegovo rešenje imaju svoje mesto u istoriji jer je to bio prvi primer primene principa minimuma u opisivanju fizičkih pojava.
Napomenimo da neki moderni udžbenici opisuju problem kroz različite praktične probleme. Na primer, prava k se uzima za železničku prugu dok tačke A i B postaju gradovi, tačka C je buduća železnička stanica koju treba sagraditi, a pitanje glasi: Gde treba graditi železničku stanicu tako da je ukupna dužina puteva kojima su gradovi spojeni sa stanicom najkraća?

(Sunset Train, Vladimir Petković)
U vezi sa opisivanim dajemo zanimljiv geodezijski problem koji je postavio najveći engleski sastavljač zanimljivih problema i zagonetki Henri Dudeni (1857–1931) u svojoj knjizi Modern Puzzles (London, 1926): Na spoljašnjoj strani čaše cilindričnog oblika (otvorenoj gore) u tački A nalazi se muva, a na unutrašnjoj strani u tački B kap meda. Kojim putem treba da ide muva da bi što pre stigla do meda? Podrazumeva se da muva ne leti do meda već ide po površinama čaše (spoljnoj do ivice a zatim po unutrašnjoj), kao i da je debljina čaše zanemarljiva.
Označimo pozicije muve i meda tačkama A i B. Ako ove dve tačke leže na istoj izvodnici valjka, rešenje je očigledno te ćemo nadalje pretpostaviti da to nije slučaj. Razvijeni omotač valjka daje pravougaonik (slika 4a).
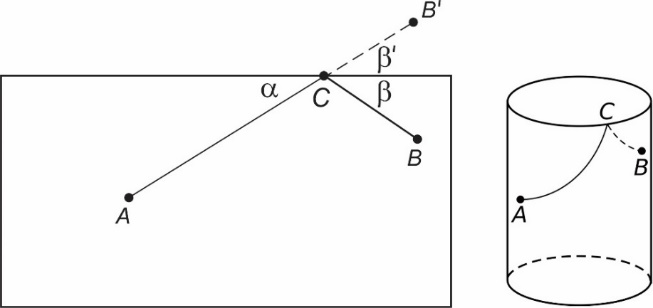
a) b)
Slika 4 Muva i kap meda
Problem se sada svodi na određivanje najkraćeg puta ACB, gde je C tačka na ivici čaše. U stvari, ovo je Heronov problem i rešenje koristi simetričnu tačku B’ tačke B u odnosu na ivicu čase. Upadni ugao α jednak je odbojnom uglu β (= β’). Muva će puziti po površini čase duž dva luka cilindrične spirale (slika 4b), prelazeći preko ivice čaše u tački C.
Heronov princip se, takođe, može uspešno primeniti za nalaženje najkraćeg puta u sledećoj situaciji opisanoj u nekoliko knjiga na ruskom i engleskom jeziku. Autor ovog priloga uvrstio je ovaj zadatak u svoju knjigu Famous Puzzles of Great Mathematics (American Mathematical Society, 2009), koja pripada i istoriji matematike i rekreativnoj matematici.
Željan odmora od buke velegrada i španskih, indijskih i turskih TV serija, mladi avanturista otišao je na odmor u Afriku. Posle kraćeg lutanja pronašao je divno mesto na ušću dveju reka koje su pravile poluostrvo u obliku oštrog ugla (sl. 5). Svakog dana avanturista napušta svoju kolibu (C), ide do jedne obale (A) poluostrva da posmatra vaterpolo-meč između lokalnih plemena, zatim ide do druge obale (B) da bere lotosove cvetove i eventualno pomiluje svog omiljenog nilskog konja, a potom se vraća u kolibu. Ove njegove šetnje idu približno istom trasom, ali nisu i najkraće. Koji put on treba da izabere da bi ukupan put CABC bio najkraći?

Slika 5 Avanturista na poluostrvu (Vladimir Petković)
Neka poluprave pA i pB označavaju obale reka i neka je sa C označena pozicija kolibe. Neka su CA i CB tačke simetrične tački C u odnosu na poluprave pA i pB (sl. 6).
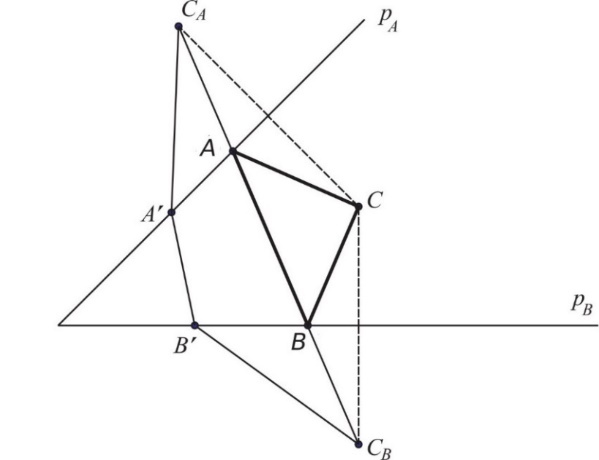
Slika 6 Avanturista na poluostrvu – rešenje
Spojimo tačke CA i CB i označimo sa A i B presečne tačke duži CACB i polupravih pA i pB. Presečne tačke A i B određuju mesta na obalama reka koja obezbeđuju najkraći put CACB avanturiste. Zaista, ako su A’ i B’ proizvoljne tačke na pA i pB, tada je
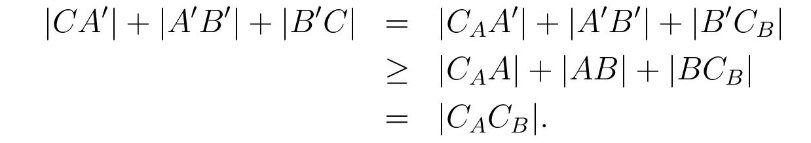
Drugim rečima, najkraći put između tačaka CA i CB ide duž prave linije. Presečne tačke A i B određuju mesta na obalama do kojih avanturista treba da trasira svoj najkraći put.
Heronov problem bio je vekovima inspiracija matematičarima da postavljaju slične i izvode razne generalizacije. Pomenućemo na kraju samo jedan dovoljno jednostavan da zainteresuje amatere za samostalno rešavanje. Slavni matematičar Pjer de Ferma (1601–1665) (uzgred, bio je pravnik koji si u slobodnom vremenu bavio matematikom) početkom 17. veka na kraju svojeg čuvenog eseja o optimizacionim problemima postavio je sledeći zadatak: U ravni su date tri tačke A, B i C tako da trougao ABC nema ugao veći od 120 stepeni. Odrediti četvrtu tačku T tako da je zbir njenih rastojanja do tri date tačke minimalan. Dakle, treba odrediti poziciju tačke T u ravni tačaka A, B i C tako da je suma |TA + TB + TC| što je moguće manja.
Fermaov problem skrenuo je pažnju eminentnom italijanskom matematičaru i fizičaru Evangelisti Toričeliju (1608–1647) koji je oko 1640. opisao geometrijsku konstrukciju za njegovo rešenje. Kasnije je napisano više naučnih radova u kojima je dato nekoliko generalizacija Heronovog problema. Ovi rezultati, a i Toričelijevo rešenje, mogu se naći u: Jakob Krarup, On Torricelli’s geometrical solution to a problem of Fermat, IMA Journal of Mathematics Applied in Business and Industry (1997) 8, 215-224. Zainteresovanim čitaocima mogu poslati kopiju u pdf-u, moja adresa je miodragpetkovic@gmail.com sa naznakom Krarup.
(Ilustracija Grand Teton, Vajoming, SAD/Miodrag Petković