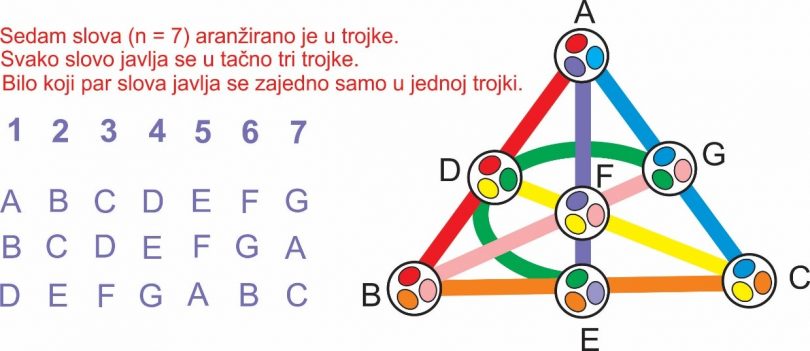
На бојном пољу 16 руских војника опколило је 12 турских војника. Сваки руски војник је пуцао само једном и сваки метак је прошао кроз турбане три турска војника. Kолико турских војника има непробушене турбане? И какве то везе има с математичким проблемом Штајнерових тројки, сликовито приказаним у насловној илустрацији?

Проф. др Миодраг Петковић
Kиркманов проблем из 19. века о 15 ученица које шетају у тројкама и слични проблем рекреативне математике довели су до развоја једне важне области комбинаторике зване блок-дизајн. Испоставило да су ови проблеми блиско повезани са различитим научним дисциплинама, као што су статистика, теорија кодова, балансирани блок дизајни, коначна геометрија, Вајерштрасове елиптичке функције, кубне криве, Штајнер-Kиркманови системи тројки, Адамарове матрице, пројективне равни. То је и тема овог прилога који садржи неколико интересантних задатака што имају и практичну вредност.
Године 1850. Томас Kиркман (1806-1895), енглески свештеник а такође експерт у теорији група и комбинаторици и члан Kраљевског друштва, поставио је у часопису Cambridge and Dublin Mathematical Journal (Vol. 2, стр. 191-204) следећи проблем: Петнаест ученица сваког дана иде у шетњу груписане у тројке. Направити такав распоред тројки да у седам узастопних дана сваки пар ученица прошета заједно једном и само једном. Другим речима, свака девојка у току седмице треба да прошета са свим својим другарицама, али са сваком само једном заједно у тројци.
Поменимо да је Kиркман формулисао овај проблем решавајући задатак који је поставио Весли Вулхауз 1844. у оквиру наградног такмичења (објављен у периодичном магазину Lady’s and Gentlemen’s Diary. Kиркман је решио Вулхаузов задатак 1847. и реформулисао га 1850. као проблем ученица (The schoolgirl problem) у форми која је горе наведена. Овај проблем и слични, који припадају области комбинаторике званој блок-дизајн, интензивно су изучавани у 19. веку, али углавном као рекреативна математика. Kасније се испоставило да су блиско повезани са различитим научним дисциплинама, као што су статистика, теорија кодова, балансирани блок дизајни, коначна геометрија, Вајерштрасове елиптичке функције, криве трећег реда, Kиркман-Штајнерове тројке, Адамарове матрице, пројективне равни.
Загонетка са ученицама које шетају има своју предисторију у причи о фармеру који жели да засади известан број стабала у воћњаку тако да постоји r правих линија са тачно k стабала у свакој. Задатак постаје тежак ако се захтева максималан број редова (за задати број стабала n и k). За n = 15 и k = 3 овај задатак се своди на Kиркманов проблем „15 ученица у шетњи”.
Генерализација Kиркмановог проблема води до Штајнеровог система тројки, названих тако према радовима чувеног швајцарског математичара Јакоба Штајнера (1796-1863). Штајнеров систем Sn(k), ако постоји, јесте распоред н објеката по тројкама тако да се било који пар објеката јавља само једном у тројци. Постоји n(n-1)/2 парова и n(n-1)/6 тројки у Штајнеровом систему; одавде, n мора да буде конгруентно са 1 или 3 по модулу 6, то јест n = 7,9,13,15… Е. Х. Мур (Moore) је доказао 1893. да је овај услов такође довољан. Подсећамо да се за целе бројеве a и b каже да су конгруентни по модулу m (m је цео број различит од 0) ако a и b при дељењу са m дају једнаке остатке.

Томас Kиркман, Јакоб Штајнер (Wikipedia)
У Kиркмановом уопштеном проблему број дана потребан за шетње је (n-1)/2. Овај број ће бити цео једино ако је n непаран умножак броја 3, тј. ако је облика 3(2k+1) = 6m+3. Одавде добијамо низ могућих вредности 3, 9, 15, 21, итд. Поменути облик 6m+3 је потребан за решење Kиркмановог уопштеног проблема, али то није довољно. У другој половини 19. века написани су многобројни научни радови на тему Kиркмановог уопштеног проблема, али с решењима само за појединачне случајеве n. Генерално решење за произвољно n (облика 6m+3) дали су 1971. године Д. K. Реј-Чаудури и Ричард М. Вилсон са Државног универзитета Охајо. Интересантно је напоменути да је касније устављено да је пре 1971. решење дао школски учитељ Лу Ксиа Кси из Монголије, али доказ није нигде публикован тако да није ни верификован. Међутим, број базичних Штајнерових тројки Sn у генералном случају је остао непознат и дан-данас и нађен је једино за мале вредности броја n. Sn расте веома брзо: на пример, за n = 31 постоји више од базичних решења.
Случај n = 3 је тривијалан, три девојке једноставно шетају у тројци само један дан. Случај n = 9 девојака у четвородневној шетњи има јединствено основно решење дато у доњој шеми:
123 147 159 168
456 258 267 249
789 369 348 357
Још 1922. године било је познато да Kиркманов проблем 15 ученица има 80 решења, од којих 7 базичних. Постоји више метода помоћу којих је могуће одредити ова решења. Овде ћемо изложити један интересантан геометријски приступ који комбинује фиксни и ротирајући диск исте величине. Овај метод описао је Мартин Гарднер у часопису Scientific American (No 5, 1980).
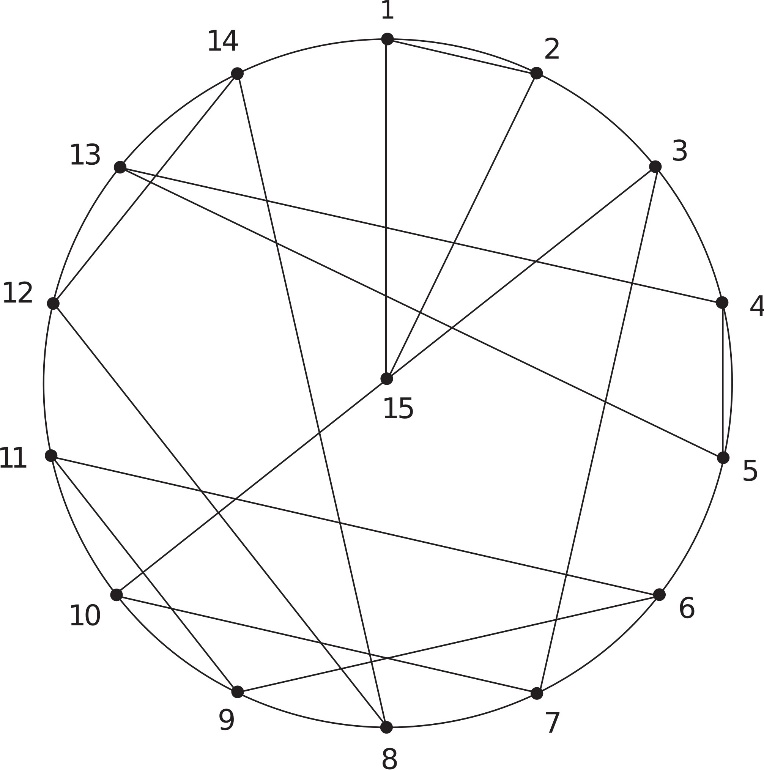
Сл. 1 Геометријско решење Kиркмановог проблема о шетњи 15 ученица
Нацртајмо кружни диск и означимо на кружници 14 пођеднако удаљених тачака обележених бројевима од 1 до 14. Исецимо од картона кружни диск исте величине и означимо обод на исти начин бројевима од 1 до 14, а центар бројем 15. Нацртајмо, затим, пречник (10,15,3) и пет неподударних троуглова (1, 2, 15), (3, 7, 10), (4, 5, 13), (6, 9, 11), (8, 12, 14), као што је приказано на слици 1. Назначени троуглови, у ствари, представљају (различите) тражене тројке и због тога не смеју бити подударни између себе. Могуће је направити седам оваквих различитих узорака који дају 7 базичних решења. Диск са овако уцртаним троугловима треба поставити на непокретни диск помоћу игле кроз центре оба диска. Поступак генерисања решења састоји се у следећем:
Почетни положај у коме се бројеви са кружница оба диска поклапају даје распоред тројки за први дан: то је (1, 2, 15), (3, 7, 10), (4, 5, 13), (6, 9, 11), (8, 12, 14). Распоред за следећих шест дана добићемо ротацијом горњег диска за две јединице у произвољном смеру. То значи да тачку на ротирајућем диску треба редом поклапати са бројевима 3, 5, 7, 9, 11 и 13 на непокретном диску (или у обратном редоследу, што је свеједно). Темена троуглова на ротирајућем диску, заједно са центром 15, налазе се наспрам бројева на непокретном диску одређујући на тај начин тражене тројке. Kомплетно решење (за узорак са слике 1) је дато у следећој табели:
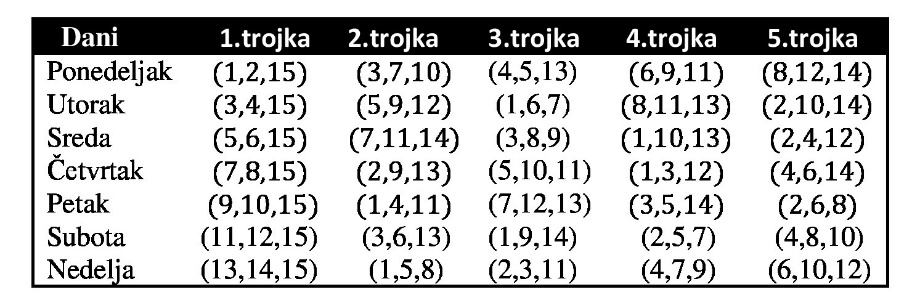
Према мишљењу великог британског математичара Џејмса Силвестера (James Joseph Sylvester, 1814-1897), који је такође био заинтересован за овај проблем, једно од најинтересантнијих решења Kиркмановог проблема дао је Б. Пирс (Pierce) у научном раду Cyclic solutions of the school-girl puzzle (The Astronomical Journal, vol. VI, 1859-1861). У својој књизи Mathematical Recreations and Essays Рауз Бол и Kоксетер дали су једно решење за свако n (облика 6m+3) мање од 100. Иначе, Силвестер се веома интересовао за Штајнерове системе тројки и радио на овој теми двадесетак година, све до своје смрти. Он је приметио да постоји (n над 3) = 455 начина да се формирају тројке од 15 ученица. Kако је 455=13 x 35, 35 = 7 дана x 5 тројки, следи да је број тројки који би евентуално могао да формира Kиркманове тројке једнак 13.
Међутим, који скуп од 35 Штајнерових система тројки задовољава Kиркманове услове? У вези с тим, Силвестер је поставио следећи проблем: Да ли се може аранжирати 455 различитих тројки у 13 различитих Штајнерових система тројки који би задовољили услове Kиркмановог проблема?
Силвестеров проблем је врло тежак и он није дочекао да види решење (умро је 1897). Одговор је нађен тек 1974. када је Р. Денисон са Лестер универзитета формулисао решење користећи рачунар (Discrete Mathematics, No 9, 1974). Програм на рачунару радио је нешто више од 7 сати.
Други Силвестеров задатак био је, такође, веома тежак: Да ли је могуће аранжирати било који коначан број тачака у равни тако да права кроз сваки скуп од две тачке може да прође и кроз трећу тачку, изузимајући случај када све тачке леже на истој правој?
Нажалост, Силвестер није видео решење ни овог свог проблема. Т. Гринвалд (1944) је био први који је дао исправно решење: одговор је да тражени узорак не постоји.
У наставку ће бити изложено неколико задатака који су засновани на Штајнер-Kиркмановим системима.
Два Дуденијева задатка (Хенри Дудени био је највећи енглески састављач логичких математичких задатака и загонетки).
Задатак 1. Дудени је поставио питање конструкције узорка у равни са 16 праваца по 3 тачке у сваком. Он је задатак формулисао у виду кратке приче из Првог светског рата чија (хумана) адаптација гласи овако: На бојном пољу 16 руских војника опколило је 11 турских војника. Сваки руски војник је пуцао само једном и сваки метак је прошао кроз турбане три турска војника. Kолико турских војника има непробушене турбане?
На основу слике 2 следи одговор: Ниједан. Позиције руских војника се налазе у продужетку сваке дужи, од којих свака садржи по три дате тачке – турске војнике.
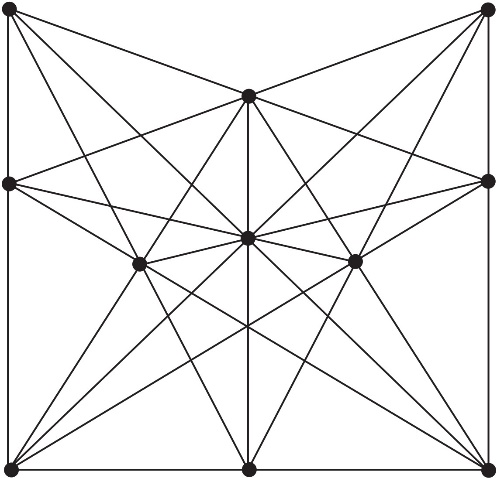
Сл. 2 11 тачака на 16 правих са тачно 3 тачке на свакој
Задатак 2. У случају када је k = 4 (Штајнеров систем Sn(4), проблем је знатно тежи. Решење са n = 16, 15 праваца по k = 4 на сваком, Дудени је приказао на слици 3. Овај пентагонални узорак подсећа на расцветани цвет Hoya carnosa (сл. 4) из фамилије Hoya који расте у источној Азији и Аустралији.
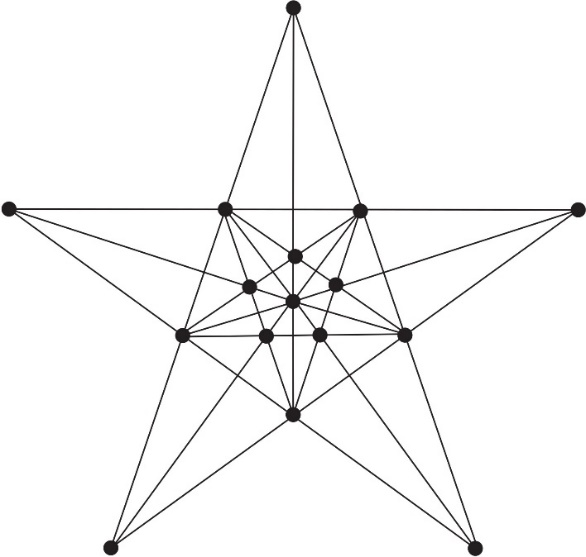

Сл. 3а 16 тачака у 15 праваца са тачно 4 тачке на свакој, 3b Узорак цвета
Проблем голф играча. У решењима су коришћена слова абедеде А-Т у првом задатку и А-X у другом задатку.
Задатак 3. 20 голфера жели да игра у четворки 5 дана. Да ли је могуц́е да сваки голфер не игра више од једном са било којим другим голфером? Одговор је да, а следећа табела даје решење (видети сајт https://mathworld.wolfram.com/SocialGolferProblem.html)
|
Dan 1 |
ABCD |
EFGH |
IJKL |
MNOP |
QRST |
|
Dan 2 |
AEIM |
BJOQ |
CHNT |
DGLS |
FKPR |
|
Dan 3 |
AGKO |
BIPT |
CFMS |
DHJR |
ELNQ |
|
Dan 4 |
AHLP |
BKNS |
CEOR |
DFIQ |
GJMT |
|
Dan 5 |
AFJN |
BLMR |
CGPQ |
DEKT |
HIOS |
Задатак 4. 24 голф играча могу играти у четворки 7 дана, као што се види из решења са сајта https://www.mathpuzzle.com/MAA/54-Golf%20Tournaments/mathgames_08_14_07.html).
Day1 ABKU IJSE QRCM DGFX HLNO PTVW
Day2 ACLV IKTF QSDN EHGR BMOP JUWX
Day3 ADMW ILUG QTEO FBHS CJNP KRVX
Day4 AENX IMVH QUFP GCBT DJKO LRSW
Day5 AFOR INWB QVGJ HDCU EKLP MSTX
Day6 AEPS IOXC QWHK BEDV FJLM NRTU
Day7 AHJT IPRD QXBL CFEW GKMN OSUV
Организатори куглања, голфа, бриџа или тениса често се баве проблемима ове врсте, немајући у виду њихову сложеност. У опшем случају проблем нема решења.