Teorija verovatnoće je puna paradoksa predviđajući ishode nekih događaja koji su, na prvi pogled a nekad i dublje, u koliziji sa zdravim razumom i logikom. To se dešava najčešće zbog toga što ljudi previđaju (ili ne shvataju) složenu zavisnost izvesnih faktora koji na direktan ili indirektan način utiču na ishod posmatranog događaja. Korišćenjem teorije verovatnoće, u ovom prilogu posmatramo teorijske šanse trojice učesnika u troboju pištoljima, pri čemu svako može da izabere na koga će pucati kada na njega dođe red. Verovatnoće pogađanja učesnika se međusobno razlikuju. Pobednik je onaj ko ostane nepogođen. Rezultat je krajnje neočekivan, ako se izabere prava strategija.

Prof dr Miodrag Petković
Sledeća priča pripada nekadašnjim vremenima kada su se nesuglasice, a posebno pitanja uvreda i odbrane časti, rešavale dvobojima. Za današnje vreme to je ne samo surov već i neshvatljiv način sporenja. Uzgred, pomenimo da je jedan od najuspešnijih duelista u istoriji bio čuveni ruski pesnik Aleksandar Puškin (1799-1837). On je učestvovao u 29 dvoboja, a u poslednjem je smrtno ranjen.

(Wikimedia Commons)
U našoj priči ne radi se o neobičnom troboju koji zbog svog paradoksalnog ishoda već decenijama zbunjuje čitaoce i predstavlja matematički hit u literaturi, a i na predavanjima iz teorije verovatnoće. Jednog hladnog zimskog dana lovci Sem, Bil i Don otišli su u lov na suanske luminiscentne jednoroge koji žive jedino u šumama provincije Suan. Do jednoroga je moguće doći haotičnim cik-cak putanjama koje neodoljivo podsećaju na Šenbergove krive, koje je otkrio ih je 1938. godine (Bilten američkog udruženja matematičara, 44, 1938). Posle dugog pešačenja šumskim stazama, na jednom proplanku ugledali su suanskog luminiscentnog jednoroga i svi istovremeno opalili iz svojih pušaka. Jednorog je smrtno pogođen, a među lovcima nastala je prepirkau vezi s tim čiji je hitac bio smrtonosan.
Svađa je predugo trajala i na kraju su se Sem, Bil i Don saglasili da spor reše pištoljima u troboju pod sledećim uslovima. Lovci se nalaze u temenima jednakostraničnog trougla. Redosled pucanja određuje se žrebom. Svako ispaljuje jedan hitac kada na njega dođe red, pri čemu može da bira u koga pucati. Obračun se prekida kada dvojica budu pogođena. Poredak u gađanju, određen žrebom pre troboja, ne menja se.
Sva trojica znaju da Sem nikad ne promašuje, Bil pogađa u 80%, a Don u 50% slučajeva. Koji od učesnika troboja ima najviše šansi da ostane nepogođen, podrazumevajući da se svaki pridržava optimalne strategije? Naći kolika je verovatnoća za svakog od lovaca da ostane nepovređen.

Troboj na groblju iz filma The Good, the Bad and the Ugly
(1967) (youtube.com)
Ovaj problem verovatno asocira neke čitaoce (naročito na ljubitelje filma) na završnu scenu iz čuvenog špageti-vesterna The Good, the Bad and the Ugly, italijanskog režisera Serđa Leonea (1967) u kome Klint Istvud (Blondie), Li van Klif (Angel Eyes) i Eli Valah (Tuco) raščišćavaju svoje račune u troboju na groblju u međusobnom revolveraškom obračunu. Naravno, uslovi tog troboja su sasvim drugačiji i u najmanju ruku nefer. Naime, Istvud je pre početka troboja ispraznio revolver Valahu (fundamentalno gnusan potez) i, naravno, koncentrisao se jedino na van Klifa čime je stekao ogromnu prednost. Dodajmo da je Klint Istvud (rođen 1930.) i u stvarnosti nadživeo ostalu dvojicu: Li van Klif je umro 1989, a Eli Valah 2014. (u 99. godini). Nakon 25 godina čuveni režiser i scenarista Kventin Tarantino snimio je kriminalistički film Reservoir Dogs(1992) sa sličnim završetkom (slika u naslovu).
Vratimo se troboju lovaca Sema, Bila i Dona. Verovali ili ne, najveću verovatnoću da ostane nepogođen u ovom troboju ima Don (oko 52%), koji važi za najgoreg strelca! Za njim sledi Sem (30%) koji uvek pogađa, a (teorijski) najmanje šanse ima Bil, oko 18%. Kako Sem i Bil, kad na njih dođe red, gađaju jedan u drugog (da bi eliminisali boljeg strelca), optimalna strategija Dona sastoji se u tome da namerno promašuje (puca u vazduh) kada na njega dođe red sve dok jedan od njegovih protivnika ne bude pogođen. Posle toga on gađa u preživelog imajući, svakako, veće preimućstvo u odnosu na njega (prednost prvog poteza).
Izračunavanje pomenutih verovatnoća zahteva poznavanje osnovnih teorema iz teorije verovatnoće. Uzimajući u obzir da je najveći broj čitalaca najverovatnije nije izučavao utoku školovanja, ova izračunavanja izostavljamo. Umesto toga opisaćemo interesantnu šemu pomoću koje se može doći do gornjih verovatnoća uz malo strpljenja.
Uvedimo najpre neke oznake. Tako P(A) označava verovatnoću da se desi događaj A. Označimo sa S događaj Sem je pogodio, a sa S* suprotan događaj Sem je promašio. Oznake B, B*, D i D*imaju analogno značenje u slučaju Bila i Dona. Odgovarajuće verovatnoće jednake su:
P(S) = 1, P(S*) = 1P(S) = 0,
P(B) = 4/5, P(B*) = 1P(B) = 1/5,
P(D) = 1/2 , P(D*) = 1P(D) = 1/2 .
Sve duele možemo predstaviti preko specijalnog grafa, tzv. „drveta” duela, slika 1. Ishodi pojedinih duela predstavljeni su pomoću čvorova grafa (kružići na slici 1), na primer, S → B znači da Sem pogađa Bila, D– označava da je Don promašio, a P(S!) da je na kraju troboja Sem ostao nepogođen (pobednik troboja). Analogne oznake važe i za Bila i Dona. Granama grafa su dodeljene odgovarajuće verovatnoće: P(S B) = 1, P(D) = 1/2 itd.
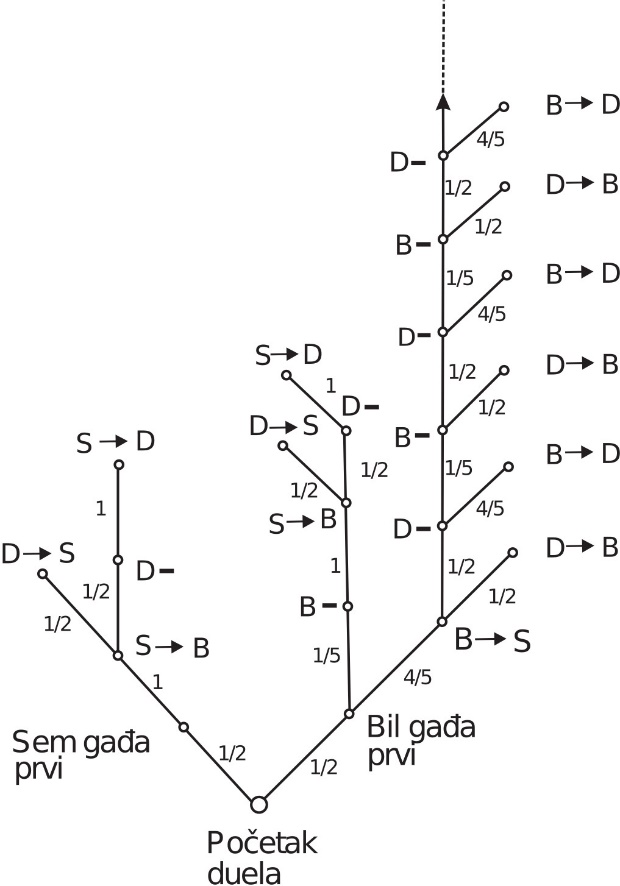
Sl. 1 Graf troboja
U početku „stablo” drveta se grana. Ovo prozilazi iz činjenice da, ako prvi gađa Don, on to čini s namerom da promaši, posle čega ostaju dve mogućnosti: gađa ili Sem ili Bil (obojica sa namerom da pogode jedan drugog). U cilju određivanja šansi Bila, Dona i Sema da iz troboja izađu nepogođeni, potrebno je sprovesti sledeći postupak:
- Krajnje čvorove na podgranama posmatrane grane treba označiti imenom osobe koja je ostala nepogođena.
- Idući od krajnjih čvorova svake od podgrana prema korenu drveta, uzimajući pritom u obzir samo čvorove označene istim imenom (i to imenom onog strelca za koga tražimo verovatnoću da nepogođen izađe iz troboja), množimo verovatnoće naznačene na svim granama puta na koji nailazimo. Dobijeni proizvod predstavlja verovatnoću događaja naznačenog na krajnjem čvoru posmatrane grane (npr. Bil pogađa Dona (B → D) ili Don pogađa Sema (D → S) itd.).
- Zbir svih proizvoda verovatnoća koje se odnose na isti događaj (npr. Bil pogađa Dona (B → D) daje verovatnoću za svakog od učesnika u troboju. Pri izračunavanju ove verovatnoće za Bila i Dona javlja se beskonačno mnogo podgrana. Međutim, pomoću grafa se lako utvrđuje zakonitost za opšti član dobijenog beskonačnog reda (preciznije, geometrijskog reda sa količnikom 1/10).
Na ovaj način se dobijaju verovatnoće za pobedu svakog od učesnika troboja:
P(S!) = 3/10 = 0.3 (30%),
P(B!) = 8/45 = 0.17777… (oko 18%),
P(D!) = 47/90 = 0.52222… (oko 52%).
Kada su jednog poznatog matematičara pitali da li je iznenađen paradoksalnim rešenjem problema troboja, odgovorio je: „Ne znam šta da mislim. Ali kad dobro razmislim, mislim da nije ispalo onako kako sam mislio.” Na njegovom mestu, čuveni književnik Oskar Vajld bi rekao: „Ne mogu da ne poverujem – jer je neverovatno!”
U prilogu je razmatran jedan paradoks objašnjen teorijom verovatniće, koji ne mora da se desi u stvarnosti. U nastavku je izložen paradoks koji se desio u stvarnosti i, što je zanimljivo, tankom niti povezan je sa opisanim zadatkom o neobičnom troboju. Ovaj nimalo lak zadatak postavio sam studentima najbolje generacije u istoriji Elektronskog fakulteta u Nišu (upisani 1989) kao jedan od pripremnih zadataka za ispit iz matematike na drugoj godini studija ne očekujući da će ga iko rešiti. Ipak, desilo se! Već sutradan studentkinja Jelena Vučković (rođena 1971) dostavila je tačno rešenje! Uzimajući u obzir više elemenata, ona je verovatno najbolji student u istoriji Niškog univerziteta i prva je ostvarila prosek 10 na Elektronskom fakultetu, i to u vreme kada nije bilo inflacije desetki.
Jelena Vučković je karijeru nastavila u inostranstvu, doktorirala je na čuvenom Kalifornijskom institutu za tehnologiju (Caltech), a danas je redovni profesor na Stenfordskom univerzitetu, jednom od najprestižnijih u svetu. Dobitica je više od 10 priznatih svetskih nagrada, a 2007. i tradicionalne Nagrade predsednika SAD kao najuspešniji naučnik mlađi od 40 godina. Ona je šef Departmana za elektrotehniku i professor na Departmanu za primenjenu fiziku gde kao šef laboratorije za kvantnu fotoniku i nanotehnologije istražuje u oblasti nanofotonike, kvantne optike, optoelektronike i kvantnih informacionih tehnologija. Takođe je konsultant u nekoliko naučnih instituta, kompanija za poluprodničku tehnoligiju i konsultant Nacionalnog fonda za nauku (NSF).Zvuči neverovatno, ovi svetski uspesi nisu bili dovoljni da bude izabrana za inostranog člana SANU.
(Ilustracija finale filma Reservoir Dogs, 1992)








