Bliže govoreći, jednu istu statističku zakonitost raspodele mi prepoznajemo, recimo, kod ponašanja jedinki u panici i kretanja akcija na berzi, kod toplotne provodljivosti metala i jezgra teških atoma, odnosno kristala i oblika proteina itako dalje, kao što i, kao matematički objekti, nalaze matrice primene u geometriji, kvantnoj teoriji, teoriji struna – i ne samo u njima.

Prof. dr Milan D. Tasić
Reč matrica, ovoga puta jednako i matematički pojam, jeste po svemu srećno odabran termin da valjano izrazi ono na šta se odnosi u nauci. Jer filozofi, naučnici bivaju na početku navedeni da nekom reči iz običnog jezika imenuju suštinu domišljenog pojma, da time, po pravilu, samo upute na nešto što će odmah zatim tačno da odrede. Inače, problem imenovanja je i soktatovski ili osnovni problem u filozofiji, a koji je prvi od filozofa-naučnika rešavao po ulicama i trgovima Atine, zapitkujući redom prolaznike: „Šta je vrlina”, „Šta je pobožnost” i slično, a koji sam nije uspevao da reši.
Ipak je ostalo to zanavek kao Sokratov zavet svakom budućem naporu u nauci da promišlja svet u pojmovima. Dodajmo i to da se u Srednjem veku naširoko raspravljalo o tzv. problemu univerzalija u nauci, a to je problem da li opšti pojmovi postoje realno u stvarnosti (realizam) ili su samo nazivi, imena (nominalizam). A jer bi, recimo, za vernika, Bog kao opšti pojam postojao u prvom slučaju, a ne u drugom itd.
Pa kad kažemo da je reč matrica srećno izabran termin da označi ono na šta se odnosi, imamo u vidu, s jedne strane, široki spektar fenomena u prirodi i društvu na koji se ona može valjano da primeni, a s druge, sam koren ove reči i njeno značenje u jeziku.
Imamo tako da je, recimo, intuitivan smisao reči prsten u govoru sasvim udaljen od odredbe istoimenog pojma u algebri, a što je u većoj ili manjoj meri slučaj s gotovo svakim od pojmova u matematici – i ne samo u njoj. Grupa, recimo, ovde nije toliko skup elemenata, koliko određeni odnos između njih, kao što imaju drugi smisao i reči ideal, filter, rešetka, snop itd. u govornom jeziku, a drugi u matematici.
Pa kad kažemo da je reč matrica srećno izabran termin da označi ono na šta se odnosi, imamo u vidu, s jedne strane, široki spektar fenomena u prirodi i društvu na koji se ona može valjano da primeni, a s druge, sam koren ove reči i njeno značenje u jeziku. Naime, pojave na koje su naročito slučajne matrice primenjive kreću se od samog haosa u prirodi, preko svake od nauka – matematike, fizike, hemije i drugih, pa sve do cunamija ili položaja drveća u šumi, odnosno čekanja metroa na stanici ili rasporeda automobila duž ulice. Bliže govoreći, jednu istu statističku zakonitost raspodele mi prepoznajemo, recimo, kod ponašanja jedinki u panici i kretanja akcija na berzi, kod toplotne provodljivosti metala i jezgra teških atoma, odnosno kristala i oblika proteina itako dalje, kao što i, kao matematički objekti, nalaze matrice primene u geometriji, kvantnoj teoriji, teoriji struna – i ne samo u njima.
A ta najšira primena njihova daje za pravo invenciji reči matrica, čiji je koren mat u mnoštvu jezika isti kao i koren naših reči majka (mati), ali i reči materija, materica i sl. Kao što je i u starogrčkom jeziku to reč meter, u latinskom mater, u engleskom mother itd.
Inače, matrice u matematici su šeme brojeva poređanih vodoravno i uspravno u okviru neke male (ili srednje) zagrade. Brojevi poređani vodoravno čine redove, a uspravno – kolone matrice, pa ako ima ona m redova i n kolona, kažemo da je dimenzija (ili tip) matrice m×n. Potom, ona je kvadratna, za m=n, simetrična ako su joj elementi simetrično raspoređeni u odnosu na glavnu dijagonalu, a hermitska onda kada su elementi, kao konjugovano-kompleksni brojevi, simetrično raspoređeni u odnosu na istu dijagonalu. Inače, njih obeležavamo velikim slovima latinice A, B, C…
Imamo zatim da ako je data matrica A i skalar k, novu matricu kA možemo da dobijemo tako što svaki elemenat A pomnožimo sa k. Ili pak da od dve matrice A i B – ali istog tipa – dobijemo matricu
C, njihov zbir A+B, kao i od matrice A tipa m×n i matrice B tipa n×p, matricu C, njihov proizvod AB, tipa m×p.
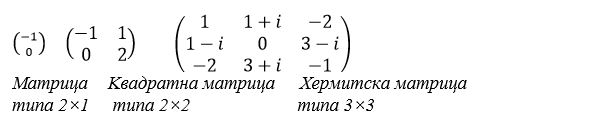
Inače, izrazitu ulogu ovi matematički objekti stiču kao operatori ili linearna preslikavanja. Reč je o mogućnosti da, recimo, neki niz od m brojeva putem određene matrice tipa m×n bude preslikan u drugi niz od n brojeva, a što bi u fizičkom svetu odgovaralo evoluciji (promeni) neke pojave od stanja određenog s m parametara do drugog stanja iste pojave s n parametara, a što bi bio i dovoljno opšt slučaj u prirodi. Na primer, radio-odašiljač bi dolazne signale frekvencija f1, f2, f3 (vektor f) modulirao u tri nove frekvencije f1*, f2*, f3* (vektor f*) radi prenosa, a što bi bilo izraženo izvesnom matricom M, tipa 3×3, pri čemu je f*=Mf.

Matrični račun je, dakle, našao mesta u proceni nivoa energije atomskih jezgara, upravo nalaženjem spektra njihovog Hamiltonovog operatora, a ne samo mputem merenja. No, ako je u slučaju lakih jezgara, poput deuterijuma, koje čine jedan proton i jedan neutron, ovaj spektar prost, nije to slučaj svakako kod teških elemenata, kao što je, recimo, uranijum 238, koji sadrži 92 protona i 146 neutrona. Stoga će pedesetih godina prošloga veka Judžin Pol Vigner (Eugene Paul Wigner), atomski fizičar i nobelovac (1963. godina), od tačnog izračunavanja nivoa energije atomskih jezgara pomeriti svoj interes na njegovu statističku raspodelu između dva vremenska trenutka. Crtajući odgovarajuće histograme, kada je uvideo bio da je kod različitih vrsta jezgara uranijuma 238, torijuma 232, kadmijuma 110 i drugih njihov tip raspodele gotovo isti (označio ga je sa GOE), kao i isti kod druge dve grupe teških metala (GUE i GSE).
I tako je to isto tajanstveno svojstvo slučajnih matrica našlo odraza i u nizu drugih otkrića u teorijskoj fizici, poput verovatnoće prelaska iz jednog u drugo kvantno stanje u teoriji struna, čija je uloga, kao što je poznato, da izmiri kvantnu mehaniku i opštu teoriju relativiteta.
Drugi (smeo) iskorak Vignerov u ovoj oblasti bio je u tome što se umesto spektra Hamiltonovog operatora (inače, suviše složenog) latio on da proučava matrice velikih dimenzija i sa slučajno odabranim elementima u njima. Reč je o elementima – u delu matrice iznad glavne dijagonale – odabranim po Gausovom zakonu verovatnoće, dok su oni ispod dijagonale ti isti elementi samo simetrično raspoređeni u odnosu na nju. Ono što je uočio bilo je pak da se kriva statističke raspodele sopstvenih vrednosti slučajnih matrica velikih dimenzija i kad ove teže u beskonačnost, približava histogramu oslobađanja energije teških jezgara, merenih difuzijom neutrona.
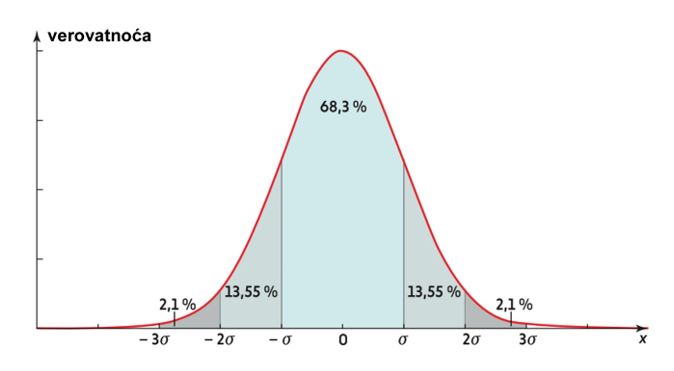
Gausova verovatnoća
Tako je ovaj tip slučajnih matrica svratio na sebe interes istraživača, ne samo u slučaju simetričnih matrica, već i hermitskih, kvaternionskih i drugih i ne samo u ovoj oblasti, već i, uopšte, u matematici, fizici, hemiji, biologiji, ekonomiji i drugim, zadobivši karakter jedne univerzalne raspodele u prirodi, a koja se približava Puasonovoj krivi raspodele slučajnih promenljivih. (vidi sliku). Ono što se pokazalo potom bilo je da se univerzalnost o kojoj je reč ne duguje zakonu verovatnoće pri izboru slučajnih promenljivih, već samoj simetriji linearnog operatora, njega kao matrice izvesne dimenzije.
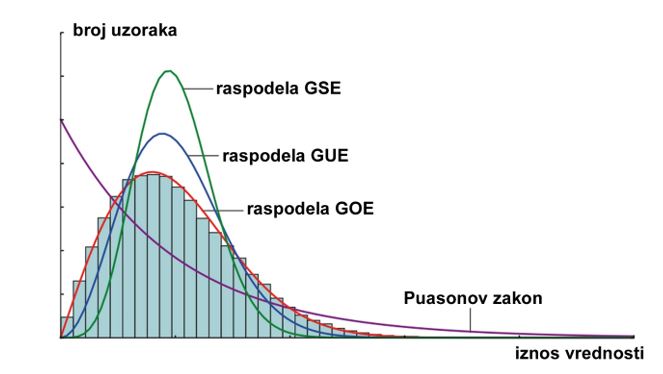
Puasonova kriva
I tako je to isto tajanstveno svojstvo slučajnih matrica našlo odraza i u nizu drugih otkrića u teorijskoj fizici, poput verovatnoće prelaska iz jednog u drugo kvantno stanje u teoriji struna, čija je uloga, kao što je poznato, da izmiri kvantnu mehaniku i opštu teoriju relativiteta. Ne bi li na taj način bila izgrađena izvesna koherentna teorija svega, kao kvantna gravitacija. Naime, pokazano je da je ona ista kao i verovatnoća slučajnih matrica čija je spektralna kriva ona površina oko koje obitavaju dimenzije struna koje se ne uočavaju u makro svetu, a kojih je više od četiri.
Recimo, najzad, da svojstva slučajnih matrica valjano objašnjavaju i različite fenomene s haotičnim procesima u prirodi, te da utoliko i privlače znatiželju stvaralaca u nauci, što mogu da se neočekivano nađu u osnovi najudaljenijih pojava i procesa u prirodi.
A s tim u vezi pomenimo i čuvenu Rimanovu (Bernhard Riemann) zeta funkciju iz 1891. godine, s beskonačno mnogo nula, čije bi poznavanje omogućilo uvid u raspored prostih brojeva u skupu svih celih brojeva. Sam Riman je istakao i hipotezu da svi prosti brojevi (sem trivijalnih) leže na istoj pravoj a što ni on ni bilo ko drugi nije uspeo da dokaže. No, sada je mnoštvo nula zeta funkcije već izračunato na računaru, da bi 1972. godine na univerzitetu Prinston dvojica matematičara H. Montgomeri (Hugh Montgomery) i F. Dajson (Freeman Dyson) pokazali da je histogram između nula zeta funkcije približno isti kao i Vignerova raspodela o kojoj smo govorili.
Zakonitost koja se prepoznaje sem toga i u najrazličitijim okolnostima u prirodi i društvu, poput one koju su opisali dvojica Čeha Milan Krbalek (Milan Krbálek) i Petr Seba (Petr Seba), a koji su istraživali vreme čekanja autobusa – kad nema reda vožnje – na nekoj stanici u gradu Kvernavaka (Cuernavaka), u Meksiku. Da bi drugi od njih ispitivao i prazan prostor između automobila parkiranih duž neke ulice u gradu i došao do istog zaključka itd.
Učestalost dolazaka
Recimo, najzad, da svojstva slučajnih matrica valjano objašnjavaju i različite fenomene s haotičnim procesima u prirodi, te da utoliko i privlače znatiželju stvaralaca u nauci, što mogu da se neočekivano nađu u osnovi najudaljenijih pojava i procesa u prirodi. Pomenimo, u tom smislu, trojicu matematičara, dobitnika Fildsove medalje: Terensa Taoa (Terence Tao), Maksima Konceviča (Maxim Kontsevitch) i Edvarda Vitena (Edward Witten), a koji su značajno doproneli razvoju teorije slučajnih matrica.